【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图 1,等腰直角四边形 ABCD,AB=BC,∠ABC=90°.
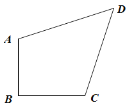
图 1
①若 AB=CD=1,AB∥CD,求对角线 BD 的长.
②若 AC⊥BD,求证:AD=CD;
(2) 如图 2,矩形 ABCD 的长宽为方程 ![]() -14x+40=0 的两根,其中(BC >AB),点 E 从 A 点出发,以 1 个单位每秒的速度向终点 D 运动;同时点 F 从 C 点出发,以 2 个单位每秒的速度向终点 B 运动,当点 E、F 运动过程中使四边形 ABFE 是等腰直角四边形时,求 EF 的长.
-14x+40=0 的两根,其中(BC >AB),点 E 从 A 点出发,以 1 个单位每秒的速度向终点 D 运动;同时点 F 从 C 点出发,以 2 个单位每秒的速度向终点 B 运动,当点 E、F 运动过程中使四边形 ABFE 是等腰直角四边形时,求 EF 的长.

图 2
参考答案:
【答案】(1)①BD=![]() ;②证明见详解;(2)
;②证明见详解;(2)![]() 或
或![]()
【解析】
(1)①只要证明四边形ABCD是正方形即可解决问题;
②只要证明△ABD≌△CBD,即可解决问题;
(2)先解方程,求出AB和BC的长度,然后根据题意,讨论当AB=AE,或AB=BF时,四边形ABFE是等腰直角四边形.当AB=AE=4时,连接EF,过F作FG⊥AE,交AE于点G,可得运动的时间为4s,可得CF=8,然后得到GE=2,利用勾股定理得到EF的长度;当AB=BF=4时,连接EF,过点E作EH⊥BF,交BF于点H ,可得CF=6,运动的时间为3s,可得AE=3,然后得到FH=1,利用勾股定理求得EF的长度.
解:(1)①∵AB=CD=1,AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形,
∵∠ABC=90°,
∴四边形ABCD是正方形,
∴BD=AC=![]() ;
;
②如图1中,连接AC、BD.
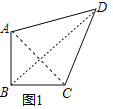
∵AB=BC,AC⊥BD,
∴∠BAC=∠BCA,
∴∠ABD=∠CBD,
∵BD=BD,
∴△ABD≌△CBD,
∴AD=CD.
(2)由AB和BC的长度是方程![]() -14x+40=0的两根,则
-14x+40=0的两根,则
解方程:![]() -14x+40=0得,
-14x+40=0得,![]() ,
,
∵BC >AB,
∴AB=4,BC=10.
根据题意,当AB=AE和AB=BF时,四边形ABFE是等腰直角四边形;
当AB=AE时,如图,连接EF,过F作FG⊥AE,交AE于点G:
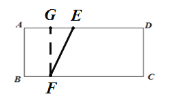
∴AB=AE=4,四边形ABFG是矩形,
∴运动的时间为:![]() ,
,
∴CF=![]() ,
,
∴BF=2=AG,
∴GE=2,GF=AB=4,
由勾股定理得:EF=![]() ;
;
当AB=BF时,如图,连接EF,过点E作EH⊥BF,交BF于点H:
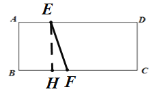
∴AB=BF=4,
∴CF=10-4=6,
则运动的时间为:![]() ,
,
∴AE=3,EH=AB=4
∴FH=4-3=1,
由勾股定理得:EF=![]() ;
;
故EF的长度为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{-1,2,3}=
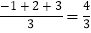 ,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________.
,min{-1,2,3}=-1,如果M{3,2x+1,4x-1}=min{2,-x+3,5x},那么x=____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为
 ﹣1.其中正确的说法是 .(把你认为正确的说法的序号都填上)
﹣1.其中正确的说法是 .(把你认为正确的说法的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019 年 7 月 1 日,《上海市生活垃圾管理条例》正式实施,生活垃圾按照“可回收物”、 “有害垃圾”、“湿垃圾”、“干垃圾”的分类标准.没有垃圾分类和未指定投放到指定垃圾桶内等会被罚款和行政处罚.垃圾分类制度即将在全国范围内实施,很多商家推出售卖垃圾分类桶,某商店经销垃圾分类桶.现有如下信息:
信息 1:一个垃圾分类桶的售价比进价高 12 元;
信息 2:卖 3 个垃圾分类桶的费用可进货该垃圾分类桶 4 个;
请根据以上信息,解答下列问题:
(1)该商品的进价和售价各多少元?
(2)商店平均每天卖出垃圾分类桶 16 个.经调查发现,若销售单价每降低 1 元,每天可多售出 2 个.为了使每天获取更大的利润,垃圾分类桶的售价为多少元时,商店每天获取的利润最大?每天的最大利润是多少?
-
科目: 来源: 题型:
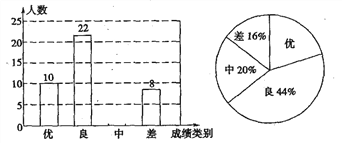
查看答案和解析>>【题目】为迎接2018年中考,我校对九年级学生进行了一次数学模拟考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如图所示的两幅不完整的统计图,请你根据统计图中提供的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)求样本中表示成绩类别为“中”的人数,并将条形统计图补充完整;
(3)我校九年级共有700人参加了这次数学考试,请估计我校九年级共有多少名学生的数学成绩可以达到优秀?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“邮扬新干线”是指从高邮站开往扬州站的公交车,中途只停靠江都站,现甲、乙、丙3名不相识的乘客同时从高邮站上车。
(1)求甲、乙、丙三名乘客在同一个站下车的概率;
(2)求甲、乙、丙三名乘客中至少有一人在江都站下车的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的
 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
相关试题

