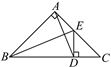
【题目】如图,△ABC是等腰直角三角形,∠BAC=90°,BE是△ABC的角平分线,ED⊥BC于点D,连接AD.
(1)请你写出图中所有的等腰三角形;
(2)若BC=10,求AB+AE的长.
参考答案:
【答案】(1)见解析;(2) AB+AE=10.
【解析】
(1)如图,根据△ABC是等腰直角三角形可知∠8=45°,由ED⊥BC可知∠7=∠8=45°,由此得到△DCE为等腰三角形;由角平分线的性质可知AE=DE,由此得到△AED为等腰三角形;同理可得△ABD为等腰三角形;
(2)由于△AED为等腰三角形,△ABD为等腰三角形,利用等腰三角形的性质即可证明AB+AE=BD+CD=BC,然后就可以求出AB+AE的长.
(1)如图,∵△ABC是等腰直角三角形,∠BAC=90°,
∴∠ABC=∠C=45°.
又∵ED⊥BC,
∴∠EDC=90°,
∴∠7=∠C=45°,
∴DE=DC,

故△DCE为等腰直角三角形.
∵BE是△ABC的角平分线,∠BAC=∠BDE=90°,
∴AE=DE,
∴△ADE为等腰三角形.
∵BE是△ABC的角平分线,
∴∠1=∠2.
又∵∠BAE=∠BDE=90°,BE=BE,
∴△ABE≌△DBE,
∴AB=DB,
∴△ABD为等腰三角形.
故图中所有的等腰三角形为△ABC,△DCE,△ADE,△ABD,共4个.
(2)由(1)可知△ADE为等腰三角形,△ABD为等腰三角形,△DCE为等腰三角形,故AB=DB,AE=DE=DC,∴AB+AE=DB+DC=BC=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填写下表,观察被开方数a的小数点与算术平方根
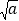 的小数点的移动规律:
的小数点的移动规律:a
0.0016
0.16
16
1600
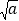
(2)根据你发现的规律填空:
①已知:
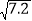 =2.683 ,
=2.683 ,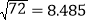 则
则 =_________,
=_________, 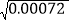 =________
=________②已知:
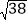 =6.164,若
=6.164,若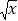 =61.64, 则x=____________,
=61.64, 则x=____________,(3)直接写出
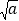 与a的大小.
与a的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.

(1)现随机转动转盘一次,停止后,指针指向2的概率为;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
游戏规则:随机转动转盘两次,停止后,指针各指向一个数字,若两数之积为偶数,则小明胜;否则小华胜. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点B,E分别在AC,DF上,BD,CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,M是边AB的中点,CH⊥AB于点H,CD平分∠ACB.

(1)求证:∠1=∠2.
(2)过点M作AB的垂线交CD的延长线于点E,连结AE,BE.求证:CM=EM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )

A. (1,﹣1) B. (2,0) C. (﹣1,1) D. (﹣1,﹣1)
-
科目: 来源: 题型:
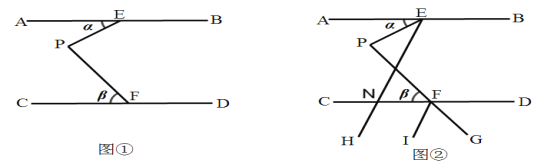
查看答案和解析>>【题目】如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFI,得到图②.
(1)在图①中,当α=20°,β=50°时,求∠EPF的度数;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请求出α与β的数量关系.
相关试题

