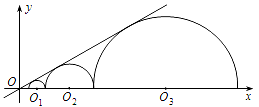
【题目】如图,圆心都在x轴正半轴上的半圆![]() ,半圆
,半圆![]() ,…,半圆
,…,半圆![]() 与直线L相切设半圆
与直线L相切设半圆![]() ,半圆
,半圆![]() ,…,半圆
,…,半圆![]() 的半径分别是
的半径分别是![]() ,
,![]() ,…,
,…,![]() ,则当直线L与x轴所成锐角为300,且
,则当直线L与x轴所成锐角为300,且![]() 时,
时,![]() = .
= .
参考答案:
【答案】![]()
【解析】
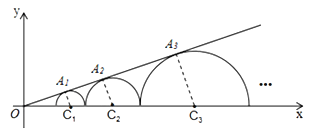
试题分析:过C1、C2、C3…、Cn作直线![]() 的垂线,垂足分别为A1、A2、A3、An,,如图,根据切线的性质得
的垂线,垂足分别为A1、A2、A3、An,,如图,根据切线的性质得![]() ,
,![]() ,
,![]() ...,
...,![]() ,再确定直线
,再确定直线![]() 与x轴正半轴的夹角为
与x轴正半轴的夹角为![]() ,接着利用两圆相切的性质得到
,接着利用两圆相切的性质得到![]() ,
,![]() ,…然后根据含30度的直角三角形三边的关系,在
,…然后根据含30度的直角三角形三边的关系,在![]() 中得到
中得到![]() ,在
,在![]() 中得到
中得到![]() ,解得
,解得![]() ,在
,在![]() 中得到6+3+
中得到6+3+![]() ,得到
,得到![]() ,再观察计算出来的半径都是3的正整数指数幂,且指数比序号小于1,于是得
,再观察计算出来的半径都是3的正整数指数幂,且指数比序号小于1,于是得![]() .
.
过C1、C2、C3…、Cn作直线![]() 的垂线,垂足分别为A1、A2、A3、An,,如图,
的垂线,垂足分别为A1、A2、A3、An,,如图,
∵a个半圆弧都与直线![]() 相切,
相切,
∴![]() ,
,![]() ,
,![]() ...,
...,![]() ,
,
∵x=1时,![]() ,
,
∴直线![]() 与x轴正半轴的夹角为
与x轴正半轴的夹角为![]() ,
,
∵a个半圆弧依次相外切,
∴![]() ,
,![]() ,…
,…
在![]() 中得到
中得到![]() ,
,
在![]() 中
中![]() ,得到
,得到![]() ,解得
,解得![]() ,
,
在![]() 中
中![]() ,得到6+3+
,得到6+3+![]() ,解到
,解到![]()
在![]() 中
中![]() ,得到18+9+r4=2 r4,解得
,得到18+9+r4=2 r4,解得![]() ,
,
由此可得:![]()
∴![]()
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋内装有大小和形状相同的一个白球和两个红球,“从中任取一球,得到白球”这个事件是( )
A. 必然事件 B. 随机事件 C. 不可能事件 D. 以上都不正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市从2018年开始大力发展旅游产业.据统计,该市2018年旅游收入约为2亿元.预计2020年旅游收入约达到2.88亿元,设该市旅游收入的年平均增长率为x,下面所列方程正确的是( )
A. 2(1+x)2=2.88 B. 2x2=2.88 C. 2(1+x%)2=2.88 D. 2(1+x)+2(1+x)2=2.88
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
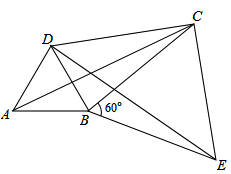
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
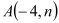 ,
,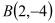 是一次函数
是一次函数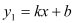 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.
的图象的两个交点.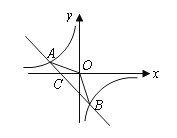
(1)求一次函数、反比例函数的关系式;
(2)求△AOB的面积.
(3)当自变量x满足什么条件时,y1>y2 .(直接写出答案)
(4)将反比例函数
 的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案)
的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
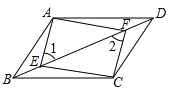
(1)求证:BE=DF;
(2)求证:AF∥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在□ABCD中,AE是BC边上的高,将
 沿
沿 方向平移,使点E与点C重合,得
方向平移,使点E与点C重合,得 .
.
(1)求证:
 ;
;(2)若
 ,当AB与BC满足什么数量关系时,四边形
,当AB与BC满足什么数量关系时,四边形 是菱形?并说明理由.
是菱形?并说明理由.注:(直角三角形中30°角所对直角边等于斜边的一半).
相关试题

