Question

【题目】如图，在平行四边形ABCD中，AE、BF分别平分∠DAB和∠ABC，交CD于点E、F，AE、BF相交于点M．

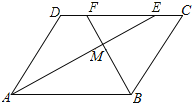
（1）试说明：AE⊥BF；

（2）判断线段DF与CE的大小关系，并予以说明．

Answer 1

【答案】（1）证明见解析（2）DF=CE，理由见解析

【解析】

试题分析：（1）利用平行四边形的性质得到AD∥BC，然后得到∠DAB+∠ABC=180°，然后根据角的平分线得出∠DAB=2∠BAE，∠ABC=2∠ABF，等量代换得出∠BAE+∠ABF=90°即可；（2）先猜想DF=CE，利用角的平分线和平行线的性质可得DE=AD，CF=BC，然后利用线段的和差关系可得出结论.

试题解析：（1）∵在平行四边形ABCD中，AD∥BC，

∴∠DAB+∠ABC=180°．

∵AE、BF分别平分∠DAB和∠ABC，

∴∠DAB=2∠BAE，∠ABC=2∠ABF．

∴2∠BAE+2∠ABF=180°．

即∠BAE+∠ABF=90°．

∴∠AMB=90°．

∴AE⊥BF．

（2）DF=CE，

∵在平行四边形ABCD中，CD∥AB，

∴∠DEA=∠EAB．

又∵AE平分∠DAB，

∴∠DAE=∠EAB．∴∠DEA=∠DAE．

∴DE=AD．

同理可得，CF=BC．

又∵在平行四边形ABCD中，AD=BC，

∴DE=CF．

∴DE﹣EF=CF﹣EF．

即DF=CE．