Question

【题目】如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于H．

（1）求证：△BCE≌△ACD；
（2）求证：FH∥BD．

Answer 1

【答案】
（1）证明：∵△ABC和△CDE都是等边三角形，

∴BC=AC，CE=CD，∠BCA=∠ECD=60°，

∴∠BCA+∠ACE=∠ECD+∠ACE，即∠BCE=∠ACD，

∴在△BCE和△ACD中，

∵ ，

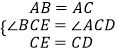∴△BCE≌△ACD （SAS）

（2）证明：由（1）知△BCE≌△ACD，

则∠CBF=∠CAH，BC=AC

又∵△ABC和△CDE都是等边三角形，且点B、C、D在同一条直线上，

∴∠ACH=180°﹣∠ACB﹣∠HCD=60°=∠BCF，

在△BCF和△ACH中，

∵ ，

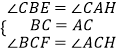∴△BCF≌△ACH （ASA），

∴CF=CH，

又∵∠FCH=60°，

∴△CHF为等边三角形

∴∠FHC=∠HCD=60°，

∴FH∥BD

【解析】（1）先根据△ABC和△CDE都是等边三角形得出BC=AC，CE=CD，∠BCA=∠ECD=60°，再由SAS定理即可得出△BCE≌△ACD；（2）由（1）知△BCE≌△ACD，可知∠CBF=∠CAH，BC=AC，再由ASA定理可知△BCF≌△ACH，可得出CF=CH，根据∠FCH=60°，可知△CHF为等边三角形，进而可得出结论．