【题目】如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.

(1)当点E为AB的中点时(如图1),则有AE DB(填“>”“<”或“=”);
(2)猜想AE与DB的数量关系,并证明你的猜想.
参考答案:
【答案】(1)=; (2)见解析
【解析】试题分析:
(1)△BCE中可证,∠BCE=30°,又EB=EC,则∠D=∠ECB=30°,所以△BCE是等腰三角形,结合AE=BE即可;
(2)过E作EF∥BC交AC于F,用AAS证明△DEB≌△ECF.
试题解析:
(1)∵△ABC是等边三角形,∴∠ABC=60°,AB=AC=BC.
∵E为AB的中点,所以∠BCE=30°.
∵ED=EC,∴∠D=∠BCE=30°,∴∠BED=30°,∴∠D=∠BED,∴BD=BE,
∴BD=AE.
(2)当点E为AB上任意一点时,AE与DB的大小关系不会改变.理由如下:
过E作EF∥BC交AC于F,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,AB=AC=BC.
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,即∠AEF=∠AFE=∠A=60°.
∴△AEF是等边三角形.∴AE=EF=AF.
∵∠ABC=∠ACB=∠AFE=60°,
∴∠DBE=∠EFC=120°,∠D+∠BED=∠FCE+∠ECD=60°.
∵DE=EC,∴∠D=∠ECD.∴∠BED=∠ECF.
在△DEB和△ECF中,
∴△DEB≌△ECF(AAS).
∴BD=EF=AE,即AE=BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P是等边三角形ABC所在平面上一点,若P和△ABC的三个顶点所组成的△PAB、△PBC、△PAC都是等腰三角形,则这样的点P的个数为( )
A.1 B.4 C.7 D.10
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2m+1)x+m2﹣4=0有两个不相等的实数根
(1)求实数m的取值范围;
(2)若两个实数根的平方和等于15,求实数m的值.
-
科目: 来源: 题型:
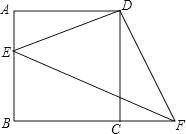
查看答案和解析>>【题目】如图,四边形ABCD是正方形,E点在AB上,F点在BC的延长线上,且CF=AE,连接DE、DF、EF.
①求证:△ADE≌△CDF;
②填空:△CDF可以由△ADE绕旋转中心 点,按逆时针方向旋转 度得到;
③若BC=3,AE=1,求△DEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式乘以多项式运算法则的依据是( )
A.乘法交换律
B.加法结合律
C.乘法分配律
D.加法交换律 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+2x﹣3经过点(1,3)
(1)求a的值;
(2)当x=3时,求y的值;
(3)求这个抛物线的对称轴和顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点P(﹣3,5)关于x轴的对称点的坐标是( )
A. (3,-5) B. (3,5) C. (5,-3) D. (-3,-5)
相关试题

