搜索
【题目】某中学团委组织学生去儿童福利院慰问，准备购买15个甲种文具和20个乙种文具，共需885元;后翻阅商场海报发现，下周甲、乙两种文具进行促销活动，甲种文具打八折销售、乙种文具打九折，且打折后两种文具的销售单价相同.
(1)求甲、乙两种文具的原销售单价各为多少元?
(2)购买打折后的15个甲种文具和20个乙种文具，共可节省多少钱?
参考答案：
【答案】（1）甲、乙两种文具的原销售单价各为27、24元；（2）共可节省129元钱．
【解析】
(1)设甲、乙两种文具的原销售单价各为x、y元，根据购买15个甲种文具和20个乙种文具，共需885元，甲种文具打八折后的销售单价=乙种文具打九折后的销售单价，列方程组求解即可；
(2)用885减去打折后购买所付的钱数即可得.
(1)设甲、乙两种文具的原销售单价各为x、y元，由题意，得
，
解得：
，
答：甲、乙两种文具的原销售单价各为27、24元；
(2)885-(15×27×0.8+20×24×0.9)=129元，
答：共可节省129元钱．
-
科目： 来源： 题型：
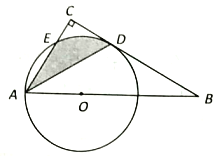
查看答案和解析>>【题目】如图，点0 为Rt△ABC斜边AB上的一点，以OA 为半径的☉O与BC切于点D，与AC 交于点E,连接AD.
(1) 求证: AD平分∠BAC;
(2)若∠BAC= 60°,OA=4,求阴影部分的面积(结果保留π).
-
科目： 来源： 题型：
查看答案和解析>>【题目】在第九章中我们研究了几种特殊四边形，请根据你的研究经验来自己研究一种特殊四边形——筝形．
初识定义：两组邻边分别相等的四边形是筝形．
（1）根据筝形的定义，写出一种你学过的四边形满足筝形的定义的是 ．
性质研究：
（2）类比你学过的特殊四边形的性质，通过观察、测量、折叠、证明等操作活动，对如图的筝形ABCD（AB＝AD，BC＝CD）的性质进行探究，以下判断正确的有 （填序号）．
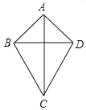
①AC⊥BD；②AC、BD互相平分；
③AC平分∠BAD和∠BCD；
④∠ABC＝∠ADC；⑤∠BAD＋∠BCD＝180°；
⑥筝形ABCD的面积为
AC×BD．（3）在上面的筝形性质中选择一个进行证明．
性质应用：
（4）直接利用你发现的筝形的性质解决下面的问题：
如图，在筝形ABCD中，AB＝BC，AD＝CD，点P是对角线BD上一点，过P分别做AD、CD垂线，垂足分别为点M、N．当筝形ABCD满足条件 时，四边形PNDM是正方形？请说明理由．
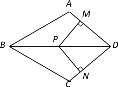
判定方法：
（5）回忆我们学习过的特殊四边形的判定方法（如四边相等的四边形是菱形），用文字语言写出筝形的一个判定方法（除定义外）： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将直线y=3x+1向下平移1个单位长度，得到直线y=3x +m,若反比例函数
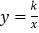的图象与直线y=3x+m相交于点A，且点A 的纵坐标是3.(1)求m和k的值;
(2) 直接写出方程
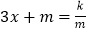的解:(3) 结合图象求不等式
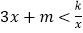的解集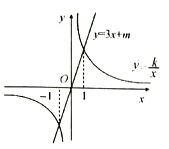
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AD//BC,BD=BC,∠ABC=900；
(1)画出
的高CE;；(2)请写出图中的一对全等三角形(不添加任何字母)，并说明理由；
(3)若
，求DE的长. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知∠ABC=
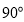,D是直线AB上的一点，AD=BC，连结DC.以DC为边，在∠CDB的同侧作∠CDE，使得∠CDE=∠ABC，并截取DE=CD，连结AE.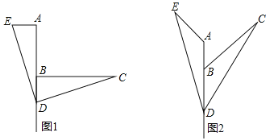
(1)求证:
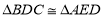;并判断AE和BC的位置关系，说明理由；(2)若将题目中的条件“∠ABC=900”改成“∠ABC=x0(0<x<180)”,
①结论“
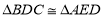”还成立吗?请说明理由；②试探索:当
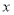的值为多少时，直线AE⊥BC. -
科目： 来源： 题型：
查看答案和解析>>【题目】2018年12月4日是第五个国家宪法日，也是第一个“宪法宣传周”．甲、乙两班各选派10名学生参加宪法知识竞赛（满分100分），成绩如下：
成绩
85
90
95
100
甲班参赛学生/人
1
1
5
3
乙班参赛学生/人
1
2
3
4
分别求甲、乙两班参赛学生竞赛成绩的平均数和方差．
相关试题
