【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)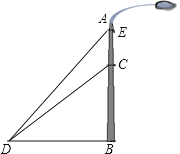
参考答案:
【答案】解:设BD=x米,则BC=x米,BE=(x+2)米,
在Rt△BDE中,tan∠EDB= ![]() ,
,
即 ![]() ,
,
解得,x≈6.06,
∵sin∠EDB= ![]() ,
,
即0.8= ![]() ,
,
解得,ED≈10
即钢线ED的长度约为10米
【解析】根据题意,可以得到BC=BD,由∠CDB=45°,∠EDB=53°,由三角函数值可以求得BD的长,从而可以求得DE的长.本题考查解直角三角形的应用,解题的关键是明确题意,利用三角函数值求出相应的边的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠B=∠C.
(1)若AD∥BC,则AD平分∠EAC吗?请说明理由.
(2)若∠B+∠C+∠BAC=180°,AD平分∠EAC,则AD∥BC吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小军两人一起做游戏,游戏规则如下:每人从1,2,…,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于他们各自选择的数,就在做一次上述游戏,直至决出胜负.若小军事先选择的数是5,用列表或画树状图的方法求他获胜的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过点A(2,0)的两条直线
 ,
, 分别交
分别交 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB= .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求
 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某一周某种股票每天的收盘价(收盘价:股票每天交易结束时的价格)

(1)填表,并回答哪天收盘价最高?哪天收盘价最低?
(2)最高价与最低价相差多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)指出数轴上 A、B、C、D、E 各点分别表示什么数;
(2)按从小到大顺序排列,将它们用“<”号连接起来;
(3)写出离 C 点 3 个单位的点表示的数;
(4)写出离 C 点 m 个单位的点表示的数(m>0).

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题是,有如下思路:连接AC.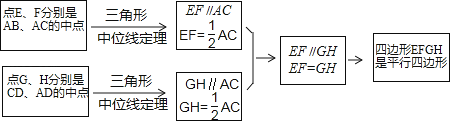
结合小敏的思路作答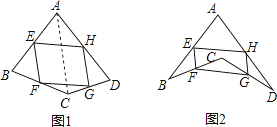
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由;参考小敏思考问题方法解决一下问题:
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
相关试题

