【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④S四边形AEPF= ![]() S△ABC , 当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( )
S△ABC , 当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( ) 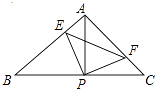
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解:∵AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,
∴AP⊥BC,AP= ![]() BC=PB,∠B=∠CAP=45°,
BC=PB,∠B=∠CAP=45°,
∵∠APF+∠FPA=90°,∠APF+∠BPE=90°,
∴∠BPE=∠APF,
在△BPE和△APF中, ,
,
∴△PFA≌△PEB(ASA),即结论①正确;
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP= ![]() BC,
BC,
又∵EF不一定是△ABC的中位线,
∴EF≠AP,故结论②错误;
∵△PFA≌△PEB,
∴PE=PF,
又∵∠EPF=90°,
∴△PEF是等腰直角三角形,故结论③正确;
∵△PFA≌△PEB,
∴S△PFA=S△PEB ,
∴S四边形AEPF=S△APE+S△APF=S△APE+S△BPE=S△APB= ![]() S△ABC , 故结论④正确;
S△ABC , 故结论④正确;
综上,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),始终正确的有3个结论.
故选(C)
根据图形旋转的性质,等腰直角三角形的性质及全等三角形的判定定理,得出△APF≌△BPE,再结合全等三角形的性质对题中的结论逐一判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(m+1)x2的图象开口向下,则m_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+2mx+9是一个多项式的平方,则m的值为( )
A. 6 B. 3 C. ±3 D. ±6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程变形属于移项的是( )
A.由﹣2y﹣5=﹣1+y,得﹣2y﹣y=5﹣1
B.由﹣3x=﹣6,得x=2
C.由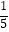 y=2,得y=10
y=2,得y=10
D.由﹣2(1﹣2x)+3=0,得﹣2+4x+3=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D , OE⊥AC于E , OF⊥AB于F , 且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( ).
A.2cm,2cm,2cm
B.3cm,3cm,3cm
C.4cm,4cm,4cm
D.2cm,3cm,5cm -
科目: 来源: 题型:
查看答案和解析>>【题目】小明每天从家去学校上学行走的路程为900米,某天他从家去上学时以每分30米的速度行走了450米,为了不迟到他加快了速度,以每分45米的速度行走完剩下的路程,设该天小明上学行走t分时行走的路程为S米,则当l5<t≤25时,s与t之间的函数关系是( )
A.s=30t
B.s=900-30t
C.S=45t-225
D.s=45t-675 -
科目: 来源: 题型:
查看答案和解析>>【题目】小虎同学在计算a+2cos60°时,因为粗心把“+”看成“-”,结果得2006,那么计算a+2cos60°的正确结果应为 .
相关试题

