【题目】如图,抛物线![]() 交x轴于A、B两点(点A在点B的左侧),
交x轴于A、B两点(点A在点B的左侧),![]() .
.
(1)求抛物线的函数表达式;
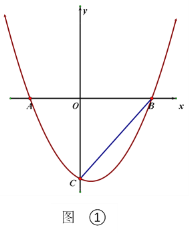
(2)如图①,连接BC,点P在抛物线上,且∠BCO=![]() ∠PBA.求点P的坐标
∠PBA.求点P的坐标
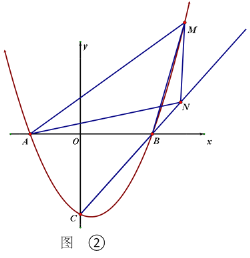
(3)如图②,M是抛物线上一点,N为射线CB上的一点,且M、N两点均在第一象限内,B、N是位于直线AM同侧的不同两点,![]() ,点M到
,点M到![]() 轴的距离为2L,△AMN的面积为5L,且∠ANB=∠MBN,请问MN的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
轴的距离为2L,△AMN的面积为5L,且∠ANB=∠MBN,请问MN的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】(1)![]() ;(2)P
;(2)P ![]() 或
或![]() ;(3)MN的为定值,定值为5
;(3)MN的为定值,定值为5
【解析】
(1)由函数解析式![]() 可确定A(
可确定A(![]() ,0),B
,0),B![]() ,再由
,再由![]() ;列出关于
;列出关于![]() 的方程即可求解;
的方程即可求解;
(2)作线段BC的垂直平分线交![]() 轴于点D,此时DC=DB,构造∠ODB=2∠BCO=∠PBA,将∠BCO=
轴于点D,此时DC=DB,构造∠ODB=2∠BCO=∠PBA,将∠BCO=![]() ∠PBA条件转化为
∠PBA条件转化为![]() ,然后设P
,然后设P![]() ,根据
,根据![]() 列方程求解即可;
列方程求解即可;
(3)由已知可求得![]() ,从而可得
,从而可得![]() ,进而可得点B、N到直线AM的距离相等,所以
,进而可得点B、N到直线AM的距离相等,所以![]() ∥BN,再证明
∥BN,再证明![]() (ASA)即可得到MN=AB=5.
(ASA)即可得到MN=AB=5.
解:(1)把![]() 代入抛物线
代入抛物线![]() ,得
,得![]() 或
或![]() ,
,
∵点A在点B的左侧,
∴A(![]() ,0),B
,0),B![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线的函数表达式为:![]() ;
;
(2)如图③,作线段BC的垂直平分线交![]() 轴于点D,此时DC=DB,
轴于点D,此时DC=DB,
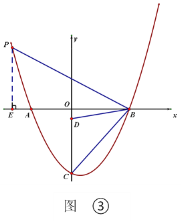
∵DC=DB,
∴∠DCB=∠DBC,
∴∠ODB=∠DCB+∠DBC=2∠BCO,
∵∠BCO=![]() ∠PBA,
∠PBA,
∴∠PBA=2∠BCO,
∴∠ODB=∠PBA,
∴![]() ,
,
设P![]() ,DC=DB=
,DC=DB=![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,

在![]() 中,
中,![]() 解得
解得![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,即
,即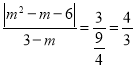 ,解得
,解得![]() ,
,
∴![]() 或
或![]() ,
,
∴点P的坐标为![]() 或
或![]() ;
;
(3)MN的为定值,定值为5;
∵![]() ,点M到
,点M到![]() 轴的距离为2L,
轴的距离为2L,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 和
和![]() 有同底AM,
有同底AM,
∴点B、N到直线AM的距离相等,
∴![]() ∥BN,
∥BN,
∴∠MAN=∠ANB,∠AMB=∠MBN,∠ABC=∠MAB,
∵∠ANB=∠MBN,
∴∠MAN=∠AMB,
∵![]() =
=![]() =
=![]() =2,
=2,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,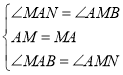 ,
,
∴![]() (ASA),
(ASA),
∴MN=AB=5,
∴MN的为定值,定值为5.

