【题目】日前一名男子报警称,在菲律宾南部发现印有马来西亚国旗的飞机残骸,怀疑是失联的马航MH370客机,马来西亚警方立即派出直升机前去查证.飞机在空中A点看见残骸C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见残骸C的俯角为45°,已知飞机的飞行度为3150米/分.
(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)
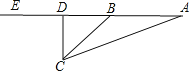
(1)求残骸到直升机航线的垂直距离CD为多少米?
(2)在B点时,机组人员接到总指挥部电话,8分钟后该海域将迎来比较大的风浪,为了能及时观察取证,机组人员决定飞行到D点立即空投设备,将残骸抓回机舱(忽略风速对设备的影响),己知设备在空中的降落与上升速度均为700米/分.设备抓取残骸本身需要6分钟,请问能否在风浪来临前将残骸抓回机舱?请说明理由.
参考答案:
【答案】(1)CD为360米;(2)能在风浪来临前将残骸抓回机舱.理由见解析
【解析】
试题分析:(1)设CD=x米,根据题意得到BD=x米,根据正切的概念列式计算即可;
(2)计算出直升飞机往返需要的时间与8分钟进行比较即可.
解:(1)设CD=x米,
∵∠DBC=45°,
∴BD=x米,
由题意得,AB=3150×![]() =840米,
=840米,
tanA=![]() ,即
,即![]() =0.3,
=0.3,
解得,x=360米
∴残骸到直升机航线的垂直距离CD为360米;
(2)直升飞机从B到D需要的时间:![]() ≈0.11分,
≈0.11分,
直升飞机从D到C和返回需要的时间:![]() ≈1分,
≈1分,
0.11+1+6=7.11<8,
∴能在风浪来临前将残骸抓回机舱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学测试中,某班50名学生的成绩分为六组,第一组到第四组的频数分别为6,8,9,12,第五组的频数是0.2,则第六组的频数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰Rt△ABC和等腰Rt△AED中,∠ACB=∠AED=90°,且AD=AC.

(1)发现:如图1,当点E在AB上且点C和点D重合时,若点M、N分别是DB、EC的中点,则MN与EC的位置关系是 ,MN与EC的数量关系是 .
(2)探究:若把(1)小题中的△AED绕点A顺时针旋转45°得到的图2,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请给予证明,若不成立,请说明理由.
(3)若把(1)小题中的△AED绕点A逆时针旋转45°得到的图3,连接BD和EC,并连接DB、EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗?若成立,请给予证明,若不成立,请说明理由.
-
科目: 来源: 题型:
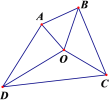
查看答案和解析>>【题目】如图,AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线。
(1)判断∠AOB与∠COD有怎样的数量关系,为什么?
(2)若∠AOD=∠BOC,AB、CD有怎样的位置关系,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A.2 B.
 C.
C.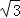 D.
D.
-
科目: 来源: 题型:
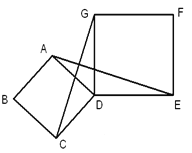
查看答案和解析>>【题目】如图所示,四边形ABCD、DEFG都是正方形,连接AE、CG。
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE=1:3,则AB= 4
 .
.
相关试题

