Question

【题目】已知：如图，二次函数的图象与x轴交于A(-2，0)，B(4，0)两点，且函数的最大值为9.

(1)求二次函数的解析式；

(2)设此二次函数图象的顶点为C，与y轴交点为D，求四边形ABCD的面积.

Answer 1

【答案】(1)、y=-+2x+8；(2)、30.

【解析】

试题分析：(1)、根据交点和最值得出顶点坐标，然后将解析式设成顶点式，然后将交点代入求出a的值；(2)、将四边形的面积转化成△AOD的面积+四边形DOEC的面积+△BCE的面积进行求解.

试题解析：(1)、由抛物线的对称性知，它的对称轴是x=1. 又∵函数的最大值为9，

∴抛物线的顶点为C(1，9). 设抛物线的解析式为y=a+9，代入B(4，0)，求得a=-1.

∴二次函数的解析式是y=-+9， 即y=-+2x+8.

(2)、

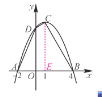
当x=0时，y=8，即抛物线与y轴的交点坐标为D(0，8).

过C作CE⊥x轴于E点.

∴S四边形ABCD=S△AOD+S四边形DOEC+S△BCE=×2×8+×(8+9)×1+×3×9=30.