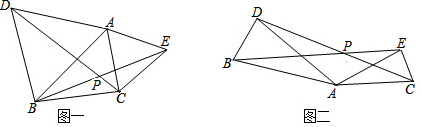
 如图一,△ABD,△AEC都是等边三角形.
如图一,△ABD,△AEC都是等边三角形.(1)求证:BE=DC;
(2)求∠DPB的度数;
(3)利用结论直接填空:
①若DC=6,点D,点C到直线BE的距离和为
3
| 3 |
3
;| 3 |
②如图二,AB=AD,AE=AC,∠BAD=∠EAC=α,则∠BPD=
α
α
.分析:(1)利用△ABD、△AEC都是等边三角形,求证△DAC≌△BAE,然后即可得出BE=DC.
(2))根据△DAC≌△BAE,得出∠ADC=∠ABE,再根据三角形的外角得出∠DPE=∠BDP+∠DBP=120°,最后根据平角的性质求出∠DPB的度数;
(3)①)根据sin∠DPM=
,DM=
×PD,CN=
•PC,再根据DM+CN=
PD+
PC,代入计算即可;
②根据SAS证出△ABD≌△AEC,得出∠ABF=∠PDF,再根据∠PFD=∠AFB,即可得出∠DPF=∠BAD=α.
(2))根据△DAC≌△BAE,得出∠ADC=∠ABE,再根据三角形的外角得出∠DPE=∠BDP+∠DBP=120°,最后根据平角的性质求出∠DPB的度数;
(3)①)根据sin∠DPM=
| DM |
| PD |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
②根据SAS证出△ABD≌△AEC,得出∠ABF=∠PDF,再根据∠PFD=∠AFB,即可得出∠DPF=∠BAD=α.
解答: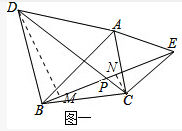 解:(1)过点D作DM⊥BE,CN⊥BE,
解:(1)过点D作DM⊥BE,CN⊥BE,
∵△ABD、△AEC都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°,
∴∠DAC=∠BAC+60°,
∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴BE=DC.
(2)∵△DAC≌△BAE,
∴∠ADC=∠ABE,
∵∠DPE=∠BDP+∠DBP
=∠BDP+∠DBA+∠ABE
=∠BDP+∠ADC+∠DBA
=60°+60°
=120°,
∴∠DPB=180°-120°=60°;
(3)①∵sin∠DPM=
,
∴DM=sin∠DPM•PD=
×PD,
同理可得:CN=
•PC,
∴DM+CN=
PD+
PC=
CD=
×6=3
;
②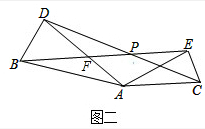 ∵∠BAD=∠EAC=α,
∵∠BAD=∠EAC=α,
∴∠BAE=∠DAC,
在△ABD和△AEC中,
,
∴△ABD≌△AEC(SAS),
∴∠ABF=∠PDF,
∵∠PFD=∠AFB,
∴∠DPF=∠BAD=α;
故答案为:3
,α.
 解:(1)过点D作DM⊥BE,CN⊥BE,
解:(1)过点D作DM⊥BE,CN⊥BE,∵△ABD、△AEC都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°,
∴∠DAC=∠BAC+60°,
∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
|
∴△DAC≌△BAE(SAS),
∴BE=DC.
(2)∵△DAC≌△BAE,
∴∠ADC=∠ABE,
∵∠DPE=∠BDP+∠DBP
=∠BDP+∠DBA+∠ABE
=∠BDP+∠ADC+∠DBA
=60°+60°
=120°,
∴∠DPB=180°-120°=60°;
(3)①∵sin∠DPM=
| DM |
| PD |
∴DM=sin∠DPM•PD=
| ||
| 2 |
同理可得:CN=
| ||
| 2 |
∴DM+CN=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
②
 ∵∠BAD=∠EAC=α,
∵∠BAD=∠EAC=α,∴∠BAE=∠DAC,
在△ABD和△AEC中,
|
∴△ABD≌△AEC(SAS),
∴∠ABF=∠PDF,
∵∠PFD=∠AFB,
∴∠DPF=∠BAD=α;
故答案为:3
| 3 |
点评:此题考查了全等三角形的判定与性质和等边三角形的性质,用到的知识点是解直角三角形、全等三角形的判定与性质、等边三角形的性质、三角形的内角和定理、对顶角相等,关键是能在较复杂的图形中找出全等的三角形.

