【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
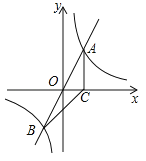
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)k=2;(2)D(5,0)或(﹣5,0)或(![]() ,0)或D(
,0)或D(![]() ,0).
,0).
【解析】试题分析:(1)首先根据反比例函数与正比例函数的图象特征,可知A、B两点关于原点对称,则O为线段AB的中点,故△BOC的面积等于△AOC的面积,都等于1,然后由反比例函数![]() 的比例系数k的几何意义,可知△AOC的面积等于
的比例系数k的几何意义,可知△AOC的面积等于![]() ,从而求出k的值;
,从而求出k的值;
(2)先将![]() 与
与![]() 联立成方程组,求出A、B两点的坐标,然后分三种情况讨论:①当AD⊥AB时,求出直线AD的关系式,令y=0,即可确定D点的坐标;②当BD⊥AB时,求出直线BD的关系式,令y=0,即可确定D点的坐标;③当AD⊥BD时,由O为线段AB的中点,可得OD=
联立成方程组,求出A、B两点的坐标,然后分三种情况讨论:①当AD⊥AB时,求出直线AD的关系式,令y=0,即可确定D点的坐标;②当BD⊥AB时,求出直线BD的关系式,令y=0,即可确定D点的坐标;③当AD⊥BD时,由O为线段AB的中点,可得OD=![]() AB=OA,然后利用勾股定理求出OA的值,即可求出D点的坐标.
AB=OA,然后利用勾股定理求出OA的值,即可求出D点的坐标.
试题解析:(1)∵反比例函数与正比例函数的图象相交于A、B两点,∴A、B两点关于原点对称,∴OA=OB,∴△BOC的面积=△AOC的面积=2÷2=1,又∵A是反比例函数![]() 图象上的点,且AC⊥x轴于点C,∴△AOC的面积=
图象上的点,且AC⊥x轴于点C,∴△AOC的面积=![]() ,∴
,∴![]() ,∵k>0,∴k=2.故这个反比例函数的解析式为
,∵k>0,∴k=2.故这个反比例函数的解析式为![]() ;
;
(2)x轴上存在一点D,使△ABD为直角三角形.将![]() 与
与![]() 联立成方程组得:
联立成方程组得: 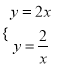 ,解得:
,解得: ![]() ,
, ![]() ,∴A(1,2),B(﹣1,﹣2),
,∴A(1,2),B(﹣1,﹣2),
①当AD⊥AB时,如图1,
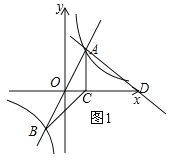
设直线AD的关系式为![]() ,将A(1,2)代入上式得:
,将A(1,2)代入上式得: ![]() ,∴直线AD的关系式为
,∴直线AD的关系式为![]() ,令y=0得:x=5,∴D(5,0);
,令y=0得:x=5,∴D(5,0);
②当BD⊥AB时,如图2,
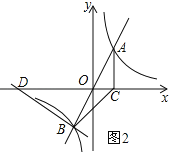
设直线BD的关系式为![]() ,将B(﹣1,﹣2)代入上式得:
,将B(﹣1,﹣2)代入上式得: ![]() ,∴直线AD的关系式为
,∴直线AD的关系式为![]() ,令y=0得:x=﹣5,∴D(﹣5,0);
,令y=0得:x=﹣5,∴D(﹣5,0);
③当AD⊥BD时,如图3,
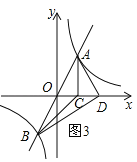
∵O为线段AB的中点,∴OD=![]() AB=OA,∵A(1,2),∴OC=1,AC=2,由勾股定理得:OA=
AB=OA,∵A(1,2),∴OC=1,AC=2,由勾股定理得:OA=![]() =
=![]() ,∴OD=
,∴OD=![]() ,∴D(
,∴D(![]() ,0),
,0),
根据对称性,当D为直角顶点,且D在x轴负半轴时,D(![]() ,0);
,0);
故x轴上存在一点D,使△ABD为直角三角形,点D的坐标为(5,0)或(﹣5,0)或(![]() ,0)或D(
,0)或D(![]() ,0).
,0).
-
科目: 来源: 题型:
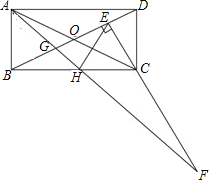
查看答案和解析>>【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有( )个.
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
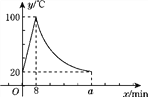
查看答案和解析>>【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图的名称;

视图 视图
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
-
科目: 来源: 题型:
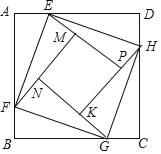
查看答案和解析>>【题目】如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
A.
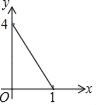 B.
B. 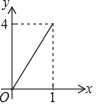 C.
C. 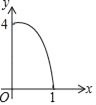 D.
D. 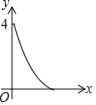
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=
ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=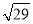 ,AE=7,tan∠EAF=
,AE=7,tan∠EAF=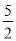 ,则线段BF的长为__________.
,则线段BF的长为__________.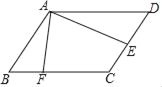
-
科目: 来源: 题型:
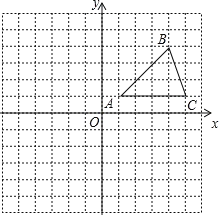
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形)。
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标;
(3)在第(2)问中,点B旋转到点B2的过程中运动的路径长是_____.
相关试题

