搜索
【题目】如图，在数轴上点A表示1，现将点A沿x轴做如下移动：第一次点A向左移动3个单位长度到达点A1，第二次将点A1向右移动6个单位长度到达点A2，第三次将点A2向左移动9个单位长度到达点A3，按照这种移动规律移动下去．第n次移动到点An，则点A2015表示的数是 ．
参考答案：
【答案】﹣6041
【解析】试题分析：序号为奇数的点在点A的左边，各点所表示的数依次减少3，序号为偶数的点在点A的右侧，各点所表示的数依次增加3，即可解答．
解：第一次点A向左移动3个单位长度至点A1，则A1表示的数，1﹣3=﹣2；
第2次从点A1向右移动6个单位长度至点A2，则A2表示的数为﹣2+6=4；
第3次从点A2向左移动9个单位长度至点A3，则A3表示的数为4﹣9=﹣5；
第4次从点A3向右移动12个单位长度至点A4，则A4表示的数为﹣5+12=7；
第5次从点A4向左移动15个单位长度至点A5，则A5表示的数为7﹣15=﹣8；
…；
则点A2015表示：﹣2﹣（2015﹣2）×3=﹣6041，
故答案为：﹣6041．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读下面的内容，再解决问题，
例题：若m2+2mn+2n2﹣6n+9=0，求m和n的值．
解：∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴（m+n）2+（n﹣3）2=0
∴m+n=0，n﹣3=0
∴m=﹣3，n=3
问题（1）若x2+2y2﹣2xy+4y+4=0，求xy的值．
（2）已知a，b，c是△ABC的三边长，满足a2+b2=10a+8b﹣41，且c是△ABC中最长的边，求c的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，D为AB的中点，AE∥CD，CE∥AB，连接DE交AC于点O．
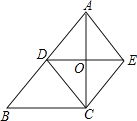
（1）证明：四边形ADCE为菱形；
（2）证明：DE=BC．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各式计算正确的是（ ）
A.a2+a2=2a4
B.5m2﹣3m2=2
C.﹣x2y+yx2=0
D.4m2n﹣m2n=2mn
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，数轴上线段AB=2（单位长度），CD=4（单位长度），点A在数轴上表示的数是﹣10，点C在数轴上表示的数是16．若线段AB以6个单位长度/秒的速度向右匀速运动，同时线段CD以2个单位长度/秒的速度向左匀速运动．
（1）问运动多少时BC=8（单位长度）？
（2）当运动到BC=8（单位长度）时，点B在数轴上表示的数是 ；
（3）P是线段AB上一点，当B点运动到线段CD上时，是否存在关系式
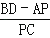=3，若存在，求线段PD的长；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图1，点A、O、B依次在直线MN上，现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转，同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转，如图2，设旋转时间为t（0秒≤t≤90秒）．
（1）用含t的代数式表示∠MOA的度数．
（2）在运动过程中，当∠AOB第二次达到60°时，求t的值．
（3）在旋转过程中是否存在这样的t，使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角（指大于0°而不超过180°的角）的平分线？如果存在，请直接写出t的值；如果不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】请列举一个单项式，使它满足系数为2，次数为3，含有字母a、b，单项式可以为 .
相关试题
