【题目】已知直线![]() 或
或![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,
两点,![]() ,则
,则![]() 的值为__________.
的值为__________.
【答案】0或4或-4
【解析】
首先对一次函数进行分类讨论,由于反比例函数![]() 的图象在第一、三象限,所以①
的图象在第一、三象限,所以①![]() 与反比例函数
与反比例函数![]() 交于
交于![]() ,
,![]() 两点,此时根据
两点,此时根据![]() ,以及直线
,以及直线![]() 与坐标轴的夹角为
与坐标轴的夹角为![]() ,可以求出
,可以求出![]() 两点的坐标为
两点的坐标为![]() ,
,![]() ,代入直线
,代入直线![]() 即可解出
即可解出![]() ;②
;②![]() 与反比例函数
与反比例函数![]() 交于
交于![]() ,
,![]() 两点,此时还应再分两种情况,i:
两点,此时还应再分两种情况,i:![]() ,设出
,设出![]() 的横坐标为
的横坐标为![]() ,则纵坐标为
,则纵坐标为![]() ,利用反比例函数的性质列出方程
,利用反比例函数的性质列出方程![]() ,解出
,解出![]() 即可求出
即可求出![]() 的值;ii:
的值;ii:![]() ,和上面同样的方法即可求解;
,和上面同样的方法即可求解;
因为直线![]() 或
或![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,①由于反比例函数
两点,①由于反比例函数![]() 的图象在第一、三象限,当
的图象在第一、三象限,当![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,且
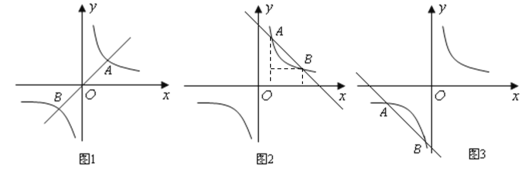
两点,且![]() 时(如图1),因为反比例函数
时(如图1),因为反比例函数![]() 的图象的两支最接近的两点
的图象的两支最接近的两点![]() 与
与![]() 之间的距离为4,此时
之间的距离为4,此时![]() ;②当直线
;②当直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点时,应分两种情况:一是在图2中,
两点时,应分两种情况:一是在图2中,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,则纵坐标为
,则纵坐标为![]() ,则有
,则有![]() ,解得
,解得![]() ,则有
,则有![]() 过点
过点![]() ,代入解析式中可得
,代入解析式中可得![]() ;同理,在图3中,可求得
;同理,在图3中,可求得![]() .
.
故答案是:0或4或-4

