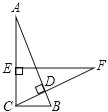
【题目】如图,Rt△ABC中,∠ACB=90°, BC=3cm, CD⊥AB于D, 在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,求AE.
参考答案:
【答案】2cm
【解析】试题分析:根据垂直的定义得到∠FEC=90°,∠ADF=90°,再根据等角的余角相等得到∠A=∠F,则可根据“AAS”可判断△ACB≌△FEC,所以AC=EF=5cm,然后利用AE=AC-EC进行计算即可.
试题解析:∵EF⊥AC,∴∠FEC=90°,∴∠F+∠FCE=90°,
∵CD⊥AB,∴∠ADC=90°,∴∠A+∠ACD=90°,∴∠A=∠F,
在△ACB和△FEC中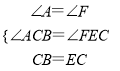 ,
,
∴△ACB≌△FEC(AAS),
∴AC=EF=5cm,
又EC=BC=3cm,
∴AE=5cm-3cm=2cm.
-
科目: 来源: 题型:
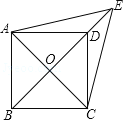
查看答案和解析>>【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过15吨(含15吨)时,每吨按政府补贴优惠价收费;每月超过15吨时,超过部分每吨按市场调节价收费.小明家1月份用水23吨,交水费35元,2月份用水19吨,交水费25元.
(1)求每吨水的政府补贴优惠价与市场调节价分别是多少;
(2)小明家3月份用水24吨,他家应交水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价-进价).这两种服装的进价,标价如表所示.
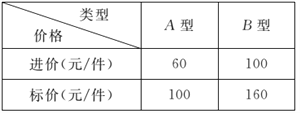
(1)求这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,D、E是△ABC中BC边上的两点,AD=AE,要证明△ABE≌△ACD,应该再增加一个什么条件?请你增加这个条件后再给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把y=
 x2的图象向上平移2个单位.
x2的图象向上平移2个单位.(1)求新图象的解析式、顶点坐标和对称轴;
(2)画出平移后的函数图象;
(3)求平移后的函数的最大值或最小值,并求对应的x的值.
相关试题

