Question

【题目】如图，△ABC是等边三角形，AB=6cm，D为边AB中点．动点P、Q在边AB上同时从点D出发，点P沿D→A以1cm/s的速度向终点A运动．点Q沿D→B→D以2cm/s的速度运动，回到点D停止．以PQ为边在AB上方作等边三角形PQN．将△PQN绕QN的中点旋转180°得到△MNQ．设四边形PQMN与△ABC重叠部分图形的面积为S（cm2），点P运动的时间为t（s）（0＜t＜3）．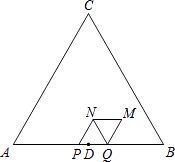

（1）当点N落在边BC上时，求t的值．
（2）当点N到点A、B的距离相等时，求t的值．
（3）当点Q沿D→B运动时，求S与t之间的函数表达式．
（4）设四边形PQMN的边MN、MQ与边BC的交点分别是E、F，直接写出四边形PEMF与四边形PQMN的面积比为2：3时t的值．

Answer 1

【答案】
（1）

解：∵△PQN与△ABC都是等边三角形，

∴当点N落在边BC上时，点Q与点B重合．

∴DQ=3

∴2t=3．

∴t=

（2）

解：∵当点N到点A、B的距离相等时，点N在边AB的中线上，

∴PD=DQ，

当0＜t＜ 时，

此时，PD=t，DQ=2t

∴t=2t

∴t=0（不合题意，舍去），

当 ≤t＜3时，

此时，PD=t，DQ=6﹣2t

∴t=6﹣2t，

解得t=2；

综上所述，当点N到点A、B的距离相等时，t=2

（3）

解：由题意知：此时，PD=t，DQ=2t

当点M在BC边上时，

∴MN=BQ

∵PQ=MN=3t，BQ=3﹣2t

∴3t=3﹣2t

∴解得t=

如图①，当 时，

S△PNQ= PQ2= t2；

∴S=S菱形PQMN=2S△PNQ= t2，

如图②，当 时，

设MN、MQ与边BC的交点分别是E、F，

∵MN=PQ=3t，NE=BQ=3﹣2t，

∴ME=MN﹣NE=PQ﹣BQ=5t﹣3，

∵△EMF是等边三角形，

∴S△EMF= ME2= （5t﹣3）2

．

（4）

解：MN、MQ与边BC的交点分别是E、F，

此时， ＜t＜ ，

t=1或 ．

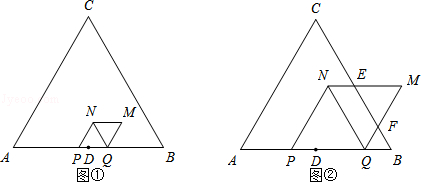
【解析】（1）由题意知：当点N落在边BC上时，点Q与点B重合，此时DQ=3；（2）当点N到点A、B的距离相等时，点N在边AB的中线上，此时PD=DQ；（3）当 时，四边形PQMN与△ABC重叠部分图形为四边形PQMN；当 时，四边形PQMN与△ABC重叠部分图形为五边形PQFEN．（4）MN、MQ与边BC的有交点时，此时 ＜t＜ ，列出四边形PEMF与四边形PQMN的面积表达式后，即可求出t的值．
【考点精析】关于本题考查的相似三角形的应用，需要了解测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解才能得出正确答案．