【题目】如图,△ABC中,∠C=90°,BC=7cm,AC=5,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.
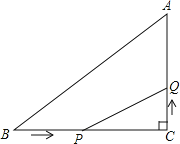
(1)若P、Q同时分别从B、C出发,那么几秒后,△PCQ的面积等于4?
(2)若P、Q同时分别从B、C出发,那么几秒后,PQ的长度等于5?
(3)△PCQ的面积何时最大,最大面积是多少?
参考答案:
【答案】(1)若P、Q同时分别从B、C出发,那么![]() 、
、![]() 秒后,△PCQ的面积等于4;
秒后,△PCQ的面积等于4;
(2)![]() 秒后,PQ的长度等于5;
秒后,PQ的长度等于5;
(3)当t=![]() 时△PCQ的面积最大,最大面积为
时△PCQ的面积最大,最大面积为![]() .
.
【解析】
试题分析:(1)分别表示出线段CP和线段CQ的长,利用三角形的面积公式列出方程求解即可;
(2)表示出线段CP和CQ后利用勾股定理列出方程求解即可;
(3)列出△PCQ的面积关于t的函数解析式,配方可得最大值.
解:(1)设t秒后△PCQ的面积等于4,根据题意得:CQ=t,BP=2t,则CP=7﹣2t,
![]() CQCP=
CQCP=![]() ×t(7﹣2t)=4,
×t(7﹣2t)=4,
整理,得:t1=![]() ,t2=
,t2=![]() ,
,
故若P、Q同时分别从B、C出发,那么![]() 、
、![]() 秒后,△PCQ的面积等于4;
秒后,△PCQ的面积等于4;
(2)若PQ的长度等于5,则PC2+QC2=PQ2,
即:(7﹣2t)2+t2=25,
整理,得:5t2﹣28t+24=0,
解得:t1=![]() ,t2=
,t2=![]() ,
,
∵CP=7﹣2t≥0,即t≤3.5,
∴t=![]() >3.5,舍去,
>3.5,舍去,
故那么![]() 秒后,PQ的长度等于5;
秒后,PQ的长度等于5;
(3)由(1)知△PCQ的面积S=![]() ×t(7﹣2t)=﹣(t﹣
×t(7﹣2t)=﹣(t﹣![]() )2+
)2+![]() ,
,
当t=![]() 时,S取得最大值,最大值为
时,S取得最大值,最大值为![]() ,
,
故当t=![]() 时△PCQ的面积最大,最大面积为
时△PCQ的面积最大,最大面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,绕某个点旋转180°后能与自身重合的有( )
①正方形;②矩形;③等边三角形;④线段;⑤角;⑥平行四边形.
A. 5个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(4分)一组数据1,1,4,3,6的平均数和众数分别是( )
A.1,3 B.3,1 C.3,3 D.3,4
-
科目: 来源: 题型:
查看答案和解析>>【题目】为筹备班级的联欢会,班长对全班学生爱吃哪几种水果作了民意调查,确定最终买什么水果,下面的调查数据中最值得关注的是( )
A. 平均数 B. 中位数 C. 众数 D. 最高值
-
科目: 来源: 题型:
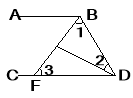
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1 +∠2 = 90°.
求证:(1)AB∥CD; (2)∠2 +∠3 = 90°;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
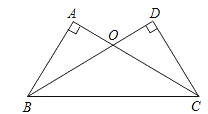
(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
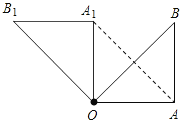
(1)线段OA1的长是 ,∠AOB1的度数是 ;
(2)连接AA1,求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
相关试题

