【题目】
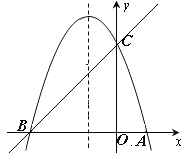
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.
⑴若直线y=mx+n经过B,C两点,求直线BC和抛物线的解析式;
⑵在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求点M的坐标;⑶设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)M(-1,2);(3)满足条件的点P共有四个,分别为
;(2)M(-1,2);(3)满足条件的点P共有四个,分别为![]() (-1,-2),
(-1,-2), ![]() (-1,4),
(-1,4), ![]() (-1,
(-1,![]() ) ,
) ,![]() (-1,
(-1,![]() ).
).
【解析】
试题分析:(1)已知抛物线y=ax2+bx+c的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,可得方程组,解方程组可求得a、b、c的值,即可得抛物线的解析式;根据抛物线的对称性和点A的坐标(1,0)可求得B点的坐标(-3,0),用待定系数法可求得直线BC的解析式;(2)使MA+MC最小的点M应为直线BC与对称轴x=-1的交点,把x=-1代入直线BC的解析式求得y的值,即可得点M的坐标;(3)分①B为直角顶点,②C为直角顶点,③P为直角顶点三种情况分别求点P的坐标.
试题解析:(1)依题意,得 解之,得
解之,得
∴抛物线解析式为![]() .
.
∵对称轴为x=-1,且抛物线经过A(1,0),
∴B(-3,0).
把B(-3,0)、C(0,3)分别直线y=mx+n,得
![]() 解之,得
解之,得![]()
∴直线BC的解析式为![]() .
.
(2)∵MA=MB,∴MA+MC=MB+MC.
∴使MA+MC最小的点M应为直线BC与对称轴x=-1的交点.
设直线BC与对称轴x=-1的交点为M,把x=-1
代入直线![]() ,得y=2.
,得y=2.
∴M(-1,2)
(3)设P(-1,t),结合B(-3,0),C(0, 3),得BC2=18,
PB2=(-1+3)2+t2=4+t2,
PC2=(-1)2+(t-3)2=t2-6t+10.
①若B为直角顶点,则BC2+PB2=PC2,即18+4+t2=t2-6t+10.
解之,得t=-2.
②若C为直角顶点,则BC2+PC2=PB2,即
18+t2-6t+10=4+t2.解之,得t=4.
③若P为直角顶点,则PB2+PC2=BC2,即
4+t2+t2-6t+10=18.解之,得t1=![]() ,t2=
,t2=![]() .
.
综上所述,满足条件的点P共有四个,分别为![]() (-1,-2),
(-1,-2), ![]() (-1,4),
(-1,4), ![]() (-1,
(-1,![]() ) ,
) ,![]() (-1,
(-1,![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两块直角三角板的直角顶点C叠放在一起.
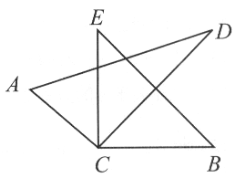
(1)若∠DCB=35°,求∠ACB的度数;
(2)若∠ACB=140°,求∠DCE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=1是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根,则2007(a+b+c)=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一个外角是70°,则它顶角的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为正方形ABCD的边BC上一动点(P与B.C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l.
(1)填表:
三边a、b、c

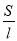
3、4、5
2
5、12、13
4
8、15、17
6
(2)如果
 ,观察上表猜想:
,观察上表猜想:  (用含有m的代数式表示).
(用含有m的代数式表示).(3)证明(2)中的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】16的平方根是( )
A.4
B.±4
C.﹣4
D.±8
相关试题

