【题目】某区在实施居民用水管理前,随机调查了部分家庭(单位:户)去年的月均用水量(单位:t),并将调查数据进行整理,绘制出如下不完整的统计图表:

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区有2000户家庭,根据此次随机抽查的数据估计,该小区月均用水量不低于20t的家庭有多少户?
(3)为了鼓励节约用水,要确定一个月均用水量的标准,超出该标准的部分按1.5倍价格收费,若要使68%的家庭水费支出不受影响,那么,你觉得家庭月均用水量应定为多少?
参考答案:
【答案】(1)见解析;(2)240户;(3)15t.
【解析】
(1)根据月用水量在0≤x<5范围的频数与百分比可得调查的总户数,从而可求得用水量在10≤x<15的频数以及20≤x<25的频率,据此补全图、表即可;
(2)用2000乘以月少水量不低于20t的家庭所占的比例即可;
(3)根据各分组的百分比进行判断即可得.
(1)∵被调查的总数量为6÷12%=50(户),
∴10≤x<15的频数为50×32%=16(户)、20≤x<25的频率为4÷50=0.08=8%,
补全图形如下:

月均用水量 | 频数 | 百分比 |
0≤x<5 | 6 | 12% |
5≤x<10 | 12 | 24% |
10≤x<15 | 16 | 32% |
15≤x<20 | 10 | 20% |
20≤x<25 | 4 | 8% |
25≤x<30 | 2 | 4% |
合计 | 50 | 100% |
(2)估计该小区月均用水量不低于20t的家庭有2000×(8%+4%)=240户;
(3)∵前三个分组的频率之和为12%+24%+32%=68%,
∴家庭月均用水量应定为15t.
-
科目: 来源: 题型:
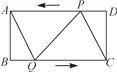
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度的速度都是1 cm/s,连结PQ,AQ,CP,设点P,Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 ( )
①2∠DCF=∠BCD; ②EF=CF; ③S△BEC=2S△CEF; ④∠DFE=3∠AEF.

A. ①②③④ B. ①②④ C. ①② D. ②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:2 sin45°﹣(﹣2012)0﹣|1﹣
sin45°﹣(﹣2012)0﹣|1﹣  |+(﹣
|+(﹣  )﹣2
)﹣2
(2)先化简,再求值: ÷(1﹣
÷(1﹣  ),其中x=0.
),其中x=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙P的圆心为P(﹣3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方.

(1)在图中作出⊙P关于y轴对称的⊙P′.根据作图直接写出⊙P′与直线MN的位置关系.
(2)若点N在(1)中的⊙P′上,求PN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌面上,先从中随机的抽取一张卡片(不放回),将该卡片正面上的数字作为十位数字,再随机的抽取一张卡片,将该卡片正面上的数字作为个位数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是_____________.

相关试题

