【题目】在桌面上,有若干个完全相同的小正方体堆成的一个几何体A,如图所示.
(1)请画出这个几何体A的三视图.


(2)若将此几何体A的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.
(3)若现在你的手头还有一些相同的小正方体可添放在几何体A上,要保持主视图和左视图不变,则最多可以添加_______个小正方体.
(4)若另一个几何体B与几何体A的主视图和左视图相同,而小正方体个数则比几何体A多1个,请画出几何体B的俯视图的可能情况(画出你认为正确的2种不同情形即可).
参考答案:
【答案】(1)见解析;(2)2;(3)4;(4)见解析
【解析】
(1)主视图可得到从左往右3列的正方形的个数依次为2,2,1;左视图得到从左往右2列的正方形的个数依次为2,2;俯视图可得从左往右3列的正方形的个数依次为2,1,1;
(2)三个面上是红色的小正方体,则为从上往下数第二行第一列的那两个;
(3)可把该几何体最多添加为2层,2行,3列共10个几何体,所以最多可添加4个正方体;
(4)可往最底层从上往下数第一行第二列,第三列,或2列之间(可根据位置不同得到多种情况);或第二层的第一列添加.
(1)主视图可得到从左往右3列的正方形的个数依次为2,2,1;左视图得到从左往右2列的正方形的个数依次为2,2;俯视图可得从左往右3列的正方形的个数依次为2,1,1;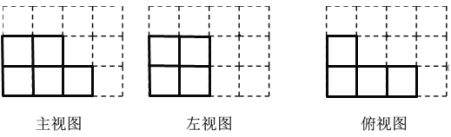 ;
;
(2)若将此几何体A的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有2个;
(3)可得该几何体最多有10个正方体,所以最多添加4个几何体;
(4)可往最底层从上往下数第一行第二列,第三列,或2列之间(可根据位置不同得到多种情况);或第二层的第一列添加.
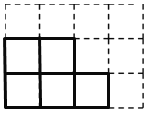
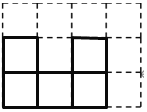
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴相交于点A(﹣1,0)和点B,与y轴交于点C,对称轴为直线x=1.
(1)求点C的坐标(用含a的代数式表示);
(2)联结AC、BC,若△ABC的面积为6,求此抛物线的表达式;
(3)在第(2)小题的条件下,点Q为x轴正半轴上一点,点G与点C,点F与点A关于点Q成中心对称,当△CGF为直角三角形时,求点Q的坐标.

-
科目: 来源: 题型:
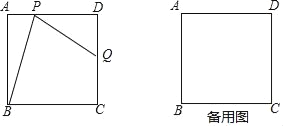
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,联结PB、PQ,且∠PBC=∠BPQ.
(1)当QD=QC时,求∠ABP的正切值;
(2)设AP=x,CQ=y,求y关于x的函数解析式;
(3)联结BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从扬州乘“K”字头列车A、“T”字头列车B都可直达南京,已知A车的平均速度为60km/h,B车的平均速度为A车的1.5倍,且走完全程B车所需时间比A车少45分钟.
(1)求扬州至南京的铁路里程;
(2)若两车以各自的平均速度分别从扬州、南京同时相向而行,问经过多少时间两车相距15km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC.
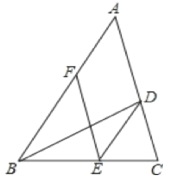
(1)求证:BE=AF;
(2)若∠ABC=60°,BD=6,求四边形ADEF的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
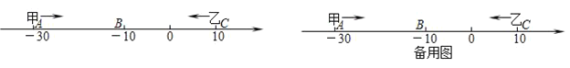
(1)甲,乙经过多少秒在数轴上相遇,并求出相遇点表示的数?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A、B、C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,一次函数y=kx+3的图象与反比例函数y=
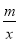 (x>0)的图象交于点P.PA⊥x轴于点A,PB⊥y轴于点B. 一次函数的图象分别交x轴、y轴于点C. 点D,且S△DBP=27,
(x>0)的图象交于点P.PA⊥x轴于点A,PB⊥y轴于点B. 一次函数的图象分别交x轴、y轴于点C. 点D,且S△DBP=27,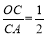
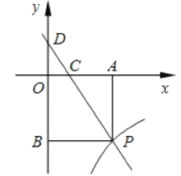
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式
相关试题

