Question

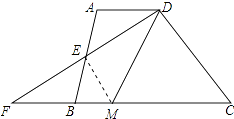
【题目】如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点M在BC边上，且∠MDF=∠ADF．

（1）求证：△ADE≌△BFE．
（2）连接EM，如果FM=DM，判断EM与DF的关系，并说明理由．

Answer 1

【答案】
（1）证明：∵AD∥BC，

∴∠ADE=∠BFE，

∵E为AB的中点，

∴AE=BE，

在△AED和△BFE中， ，

∴△AED≌△BFE（AAS）

（2）解：EM与DM的关系是EM垂直且平分DF；理由如下：

连接EM，如图所示：

由（1）得：△AED≌△BFE，

∴DE=EF，

∵∠MDF=∠ADF，∠ADE=∠BFE，

∴∠MDF=∠BFE，

∴FM=DM，

∴EM⊥DF，

∴ME垂直平分DF．

【解析】（1）由平行线的性质得出∠ADE=∠BFE，由E为AB的中点，得出AE=BE，由AAS证明△AED≌△BFE即可；（2）由△AED≌△BFE，得出对应边相等DE=EF，证明FM=DM，由三角形的三线合一性质得出EM⊥DF，即可得出结论．
【考点精析】掌握线段垂直平分线的性质是解答本题的根本，需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等．