【题目】如图,在□ABCD中,点E、F分别是BC,AD上的点,且BE=DF,对角线AC⊥AB.
(1)求证:四边形AECF是平行四边形;
(2)①当E为BC的中点时,求证:四边形AECF是菱形;
②若AB=6,BC=10,当BE长为 时,四边形AECF是矩形.
③四边形AECF有可能成为正方形吗?答: .(填“有”或“没有”)

参考答案:
【答案】(1)证明见解析;(2)①证明见解析,②3.6,③没有
【解析】试题分析: (1)首先根据平行四边形的性质可得AD∥BC,AD=BC,再证明AF=EC,可证明四边形AECF是平行四边形;
(2) ①根据直角三角形斜边上的中线等于斜边的一半可得AE=![]() CB=5,然后再根据一组邻边相等的平行四边形是菱形;
CB=5,然后再根据一组邻边相等的平行四边形是菱形;
②由矩形的性质得出∠AEC=∠AEB=90°,证出△ABE∽△CBA,得出对应边成比例,即可求出BE的长;
③根据正方形的判定即可得出.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵BE=DF,∴AF=EC,
∴四边形AECF是平行四边形;
(2)解:①∵AC⊥AB,∴∠BAC=90°,
∵E为BC的中点,∴AE=CE,
∵四边形AECF是平行四边形,
∴四边形AECF为菱形,
②∠AEC=90°,
∴∠AEB=90°=∠BAC,
∵∠B=∠B,
∴△ABE∽△CBA,
∴![]() ,
,
∴BE=![]() ;
;
故答案为:3.6;
③没有;
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下面的推理过程补充完整,并在括号内注明理由.
如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,试说明:(1)∠C=∠F;(2)AC∥DF.

解:(1)∵AD=BE(已知)
∴AD+DB=DB+BE( )
即AB=DE
∵BC∥EF(已知)
∴∠ABC=∠ ( )
又∵BC=EF(已知)
∴△ABC≌△DEF( )
∴∠C=∠F,∠A=∠FDE( )
∴AC∥DF( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②
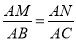 ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=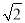 PC.其中正确的个数是( )
PC.其中正确的个数是( )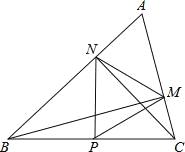
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,t的值为( )
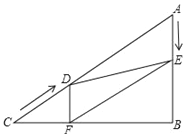
A. 20秒 B. 18秒 C. 12 秒 D. 6秒
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上则a的值是( )

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式12ab3c+8a3b的各项公因式是( )
A.4ab2
B.4abc
C.2ab2
D.4ab -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=-6x2,当x1>x2>0时,y1与y2的大小关系为____.
相关试题

