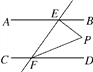
【题目】如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的平分线FP相交于点P.若∠BEP=46°,则∠EPF=________°.
参考答案:
【答案】68
【解析】由AB∥CD,根据两直线平行,同旁内角互补,即可得∠BEF+∠DFE=180°,又由EP⊥EF,∠EFD的平分线与EP相交于点P,∠BEP=46°,即可求得∠PFE的度数,然后根据三角形的内角和定理,即可求得∠EPF的度数.
解:∵AB∥CD,
∴∠BEF+∠DFE=180°,
∴EP⊥EF,
∴∠PEF=90°,
∵∠BEP=36°,
∴∠EFD=180°90°46°=44°,
∵∠EFD的平分线与EP相交于点P,
∴∠EFP =![]() ∠EFD=22°,
∠EFD=22°,
∴∠EPF=90°∠EFP=68°.
故答案为:68.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xoy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,比﹣1小的数是( )
A.﹣2B.﹣0.5C.0D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】为支援某灾区,某市民政局组织募捐了240吨救灾物资,现租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载货量和租金如下表:
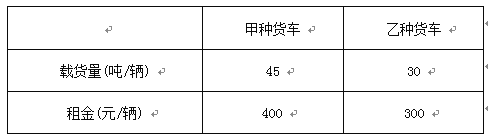
如果计划租用6辆货车,且租车的总费用不超过2 300元,求最省钱的租车方案.
-
科目: 来源: 题型:
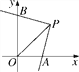
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,三角板的直角顶点P的坐标为(2,2),一条直角边与x轴的正半轴交于点A,另一直角边与y轴交于点B,三角板绕点P在坐标平面内转动的过程中,当△POA为等腰三角形时,请写出所有满足条件的点B的坐标__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛,某学校组织了一次体育知识竞赛.每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图,如图所示.
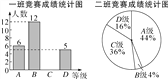
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
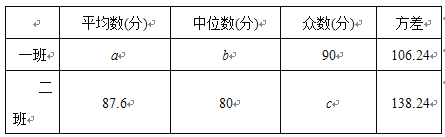
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线CB∥OA,∠C=∠OAB=100°,点E、F在线段BC上,满足∠FOB=∠AOB=α,OE平分∠COF.
(1)用含有α的代数式表示∠COE的度数;
(2)若沿水平方向向右平行移动AB,则∠OBC∶∠OFC的值是否发生变化?若变化,找出变化规律;若不变,求其比值.
相关试题

