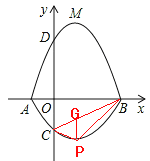
【题目】如图,在平面直角坐标系![]() 中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,
中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,![]() ),点M是抛物线C2:
),点M是抛物线C2:![]() (
(![]() <0)的顶点.
<0)的顶点.
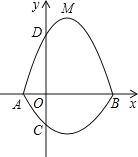
(1)求A、B两点的坐标;
(2)当△BDM为直角三角形时,求![]() 的值.
的值.
(3)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
参考答案:
【答案】(1)A(-1,0),B(3,0);(2)-![]() ;(3)P(
;(3)P(![]() ,-
,-![]() );
);![]() .
.
【解析】
试题分析: (1)将y=mx2-2mx-3m化为交点式,即可得到A、B两点的坐标;
(2)先表示出DM2,BD2,MB2,再利用DM2+MB2=BD2,即可求得m的值;
(3)先用待定系数法得到抛物线C1的解析式,过点P作PQ∥y轴,交BC于Q,用待定系数法得到直线BC的解析式,再根据三角形的面积公式和配方法得到△PBC面积的最大值.
试题解析:(1)由题意可得:y=mx2-2mx-3m=m(x-3)(x+1),
∵m≠0,
∴当y=0时,0=m(x-3)(x+1),
解得:x1=-1,x2=3,
∴A(-1,0),B(3,0);
(2)如图1,
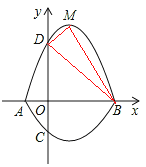
∵y=mx2-2mx-3m=m(x-1)2-4m,
∴顶点M坐标(1,-4m),
当x=0时,y=-3m,
∴D(0,-3m),B(3,0),
∴DM2=(0-1)2+(-3m+4m)2=m2+1,
MB2=(3-1)2+(0+4m)2=16m2+4,
BD2=(3-0)2+(0+3m)2=9m2+9,
当△BDM为Rt△,∠M为直角的直角三角形时,有:DM2+MB2=BD2.
DM2+MB2=BD2时有:m2+1+16m2+4=9m2+9,
解得m=-![]() (m=
(m=![]() 舍去).
舍去).
故m=-![]() 时,△BDM为以∠M为直角的直角三角形;
时,△BDM为以∠M为直角的直角三角形;
(3)设C1:y=ax2+bx+c,将A、B、C三点的坐标代入得:
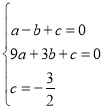 , 解得
, 解得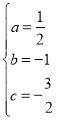 ,
,
故C1:y=![]() x2-x-
x2-x-![]() .
.
如图2:过点P作PQ∥y轴,交BC于Q,
由B、C的坐标可得直线BC的解析式为:y=![]() x-
x-![]() ,
,
设P(x,![]() x2-x-
x2-x-![]() ),则Q(x,
),则Q(x,![]() x-
x-![]() ),
),
PQ=![]() x-
x-![]() -(
-(![]() x2-x-
x2-x-![]() )=-
)=-![]() x2+
x2+![]() x,
x,
S△PBC=S△PCQ+S△PBQ=![]() PQ
PQ![]() OB=
OB=![]() ×(-
×(-![]() x2+
x2+![]() x)×3=-
x)×3=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
当x=![]() 时,S△PBC有最大值,Smax=
时,S△PBC有最大值,Smax=![]() ,
,
则![]() ×(
×(![]() )2-
)2-![]() -
-![]() =-
=-![]() ,
,
故P(![]() ,-
,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据0,1,1,x,3,4的极差是6,则这组数据的x是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:﹣1+2=1;﹣1+2﹣3+4=2;﹣1+2﹣3+4﹣5+6=3…那么﹣5+6﹣7+8﹣9+10﹣…﹣2015+2016﹣2017+2018=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了考察甲、乙两种小麦的长势,分别从中抽出20株测得其高度,并求得它们的方差分别为S甲2=3.6,S乙2=15.8,则种小麦的长势比较整齐.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣4,1)关于y轴的对称点坐标为 , 关于原点对称的点的坐标为
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正多边形的一个外角等于60°,则该正多边形的边数为( )
A.3 B.4 C.5 D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三元一次方程x+y+2z=5中,若x=﹣1,y=2,则z=_____.
相关试题

