Question

【题目】在平行四边形ABCD中，AD=BD，E为AB的中点，F为CD上一点，连接EF交BD于G．

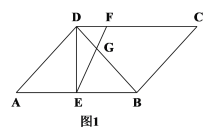
（1）如图1，若DF=DG=2，AB=8，求EF的长；

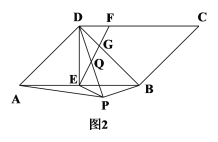
（2）如图2，∠ADB=90°，点P为平行四边形ABCD外部一点，且AP=AD，连接BP、DP、EP，DP交EF于点Q，若BP⊥DP，EF⊥EP，求证：DQ=PQ．

Answer 1

【答案】（1）；（2）见解析

【解析】

（1）利用平行线分线段成比例定理求出BG，利用勾股定理求出DE即可解决问题；

（2）如图2中，设AB交PD于点O．证明△DEQ≌△BEP（ASA），推出EQ=EP，DQ=PB，PQ=PE，由△ADE∽△ABD，可得AD2=AEAB，可得AP2=AEAB，推出△EAP∽△PAB，可得，推出PB=PE，由此即可解决问题．

解：（1）如图1中，

∵DA=DB，AE=EB，

∴DE⊥AB，

∵四边形ABCD 是平行四边形，

∴CD∥AB，

∴DE⊥CD，

∵DF∥EB，

∴，

∴，

∴BG=4，

在Rt△DEB中，∵∠DEB=90°，EB=4，DB=6，

∴DE=，

在Rt△DEF中，则有EF=；

（2）如图2中，设AB交PD于点O，

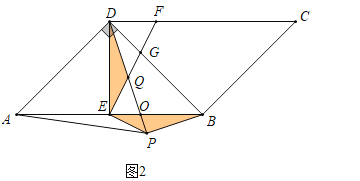
∵EF⊥PE，

∴∠PEF=∠DEB=90°，

∴∠DEQ=∠BEP，

∵DP⊥PB，

∴∠DEO=∠OPB=90°，

∵∠DOE=∠BOP，

∴∠EDQ=∠EBP，

∵△ADB是等腰直角三角形，AE=EB，

∴DE=AE=EB，

∴△DEQ≌△BEP（ASA），

∴EQ=EP，DQ=PB，

∵∠PEQ=90°，

∴PQ=PE，

∵△ADE∽△ABD，可得AD2=AEAB，

∵AD=AP，

∴AP2=AEAB，

∴，

∵∠EAP=∠BAP，

∴△EAP∽△PAB，

∴，

∴PB=PE，

∴DQ=PE，

∴DQ=PQ.