【题目】如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上的数小1,那么我们把这样的自然数叫做“相连数”,例如:234,4567,56789,......都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的和;
(2)若某个“相连数”恰好等于其个位数的576倍,求这个“相连数”.
参考答案:
【答案】(1)212;(2)这个“相连数”为:3456;
【解析】
(1)根据题意得出数字,相加即可.
(2)先由题意得出x的范围,再分类讨论列出式子即可.
(1)由题意得:最大的两位“相连数”:89;最小的三位“相连数”:123;
它们的和:89+123=212;
(2)设这个“相连数”的个位数为x.
∵1≤x≤9
∴1×576≤这个“相连数”≤9×576=5211
∴这个数可能为三位数或四位数
①当这个数为三位数时:
100(x-2)+10(x-1)+x=576x
100x-200+10x-10+x=576x
465x=﹣210
x=![]()
不符合题意,舍去
②当这个数为四位数时:
1000(x-3)+100(x-2)+10(x-1)+x=576x
1000x-3000+100x-200+10x-10+x=576x
535x=3210
x=6
∴这个“相连数”为:3456
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
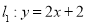 与
与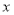 轴交于点
轴交于点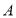 ,与
,与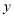 轴交于点
轴交于点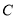 ;直线
;直线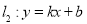 与
与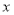 轴交于点
轴交于点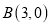 ,与直线
,与直线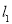 交于点
交于点 ,且点
,且点 的纵坐标为4.
的纵坐标为4.
(1)不等式
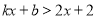 的解集是 ;
的解集是 ;(2)求直线
 的解析式及
的解析式及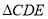 的面积;
的面积;(3)点
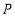 在坐标平面内,若以
在坐标平面内,若以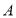 、
、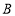 、
、 、
、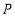 为顶点的四边形是平行四边形,求符合条件的所有点
为顶点的四边形是平行四边形,求符合条件的所有点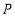 的坐标.
的坐标. -
科目: 来源: 题型:
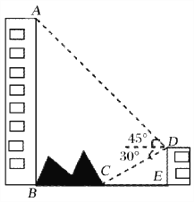
查看答案和解析>>【题目】如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上). 已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果精确到0.1m)
(参考数据:
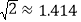 ,
,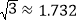 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>6且x<14,单位km)

(1)这辆出租车第三次行驶完后在离出发点的 方向;经过连续4次行驶后,这辆车所在的位置 (结果用表示);
(2)这辆出租车一共行驶了多少路程(结果用表示);当x=8时,出租车行驶的路程是多少 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
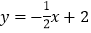 与双曲线
与双曲线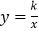 相交于点A(m,3),与x轴交于点C.
相交于点A(m,3),与x轴交于点C.(1)求双曲线的解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区. 已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知拋物线
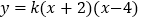 (k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线
(k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线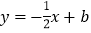 与抛物线的另一个交点为D.
与抛物线的另一个交点为D.(1)若点D的横坐标为x= -4,求这个一次函数与抛物线的解析式;
(2)若直线m平行于该抛物线的对称轴,并且可以在线段AB间左右移动,它与直线BD和抛物线分别交于点E、F,求当m移动到什么位置时,EF的值最大,最大值是多少?
(3)问原抛物线在第一象限是否存在点P,使得△APB∽△ABC?若存在,请求出这时k的值;若不存在,请说明理由.

相关试题

