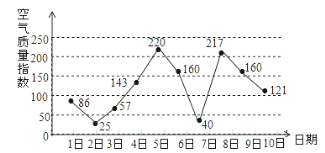
【题目】如图是某市某月1日至10日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择7月1日至7月8日中的某一天到达该市,并连续停留3天.则此人在该市停留期间有且仅有1天空气质量重度污染的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
先求出3天中空气质量指数的所有情况,再求出1天空气质量为重度污染的情况数,根据概率公式求解即可.
∵由图可知,当1号到达时,停留的日子为1、2、3号,此时为(86,25,57),3天空气质量均为优;
当2号到达时,停留的日子为2、3、4号,此时为(25,57,143),2天空气质量为优;
当3号到达时,停留的日子为3、4、5号,此时为(57,143,220),1天空气质量为重度污染;
当4号到达时,停留的日子为4、5、6号,此时为(143,220,160),1天空气质量为重度污染;
当5号到达时,停留的日子为5、6、7号,此时为(220,160,40),1天空气质量为重度污染;
当6号到达时,停留的日子为6、7、8号,此时为(160,40,217),1天空气质量为重度污染;
当7号到达时,停留的日子为7、8、9号,此时为(40,217,160),1天空气质量为重度污染;
当8号到达时,停留的日子为8、9、10号,此时为(217,160,121),1天空气质量为重度污染;
∴此人在该市停留期间有且仅有1天空气质量为重度污染的概率=![]() .
.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.

(1)在图1中以格点为顶点画一个面积为5的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、
 、
、 ;
;(3)如图3,A、B、C是小正方形的顶点,求∠ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=
 c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+ cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+
 cx+b=0必有实数根;
cx+b=0必有实数根;若x=1是“勾系一元二次方程”ax+
 cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是 ,求△ABC面积.
,求△ABC面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
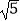 cm,且tan∠EFC=
cm,且tan∠EFC=  ,则矩形ABCD的周长是 .
,则矩形ABCD的周长是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE∥BF,AC平分∠BAE,交BF于C.

(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)求证:AD=BC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不超过8 000元,那么该商店至多购进A种纪念品几件?
相关试题

