【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF. 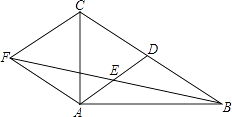
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
参考答案:
【答案】
(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中
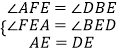
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC
(2)四边形ADCF是菱形,
证明:AF∥BC,AF=DC,
∴四边形ADCF是平行四边形,
∵AC⊥AB,AD是斜边BC的中线,
∴AD= ![]() BC=DC,
BC=DC,
∴平行四边形ADCF是菱形
【解析】(1)根据AAS证△AFE≌△DBE,推出AF=BD,即可得出答案;(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据菱形的判定推出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有4张卡片,卡片上分别标有数字1、﹣2、﹣3、4,它们除了标有的数字不同之外再也没有其它区别,小芳从盒子中随机抽取一张卡片.
(1)求小芳抽到负数的概率;
(2)若小明再从剩余的三张卡片中随机抽取一张,请你用树状图或列表法,求小明和小芳两人均抽到负数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为(
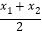 ,
,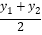 ).
).观察应用:
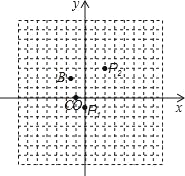
(1)如图,在平面直角坐标系中,若点P1(0,﹣1)、P2(2,3)的对称中心是点A,则点A的坐标为 ;
(2)另取两点B(﹣1.6,2.1)、C(﹣1,0).有一电子青蛙从点P1处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…则点P3、P8的坐标分别为 、 .
拓展延伸:
(3)求出点P2012的坐标,并直接写出在x轴上与点P2012、点C构成等腰三角形的点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若
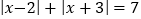 ,则
,则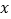 =____.
=____. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,DE垂直平分AB,分别交AB,BC于点D,E,MN垂直平分AC,分别交AC,BC于点M,N.
(1)如图①,若∠BAC = 110°,求∠EAN的度数;
(2)如图②,若∠BAC =80°,求∠EAN的度数;
(3)若∠BAC = α(α ≠ 90°),直接写出用α表示∠EAN大小的代数式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解嘉峪关初三学生体育测试自选项目的情况,从我市初三学生中随机抽取中部分学生的自选项目进行统计,绘制了扇形统计图和频数分布直方图,请根据图中信息,回答下列问题:
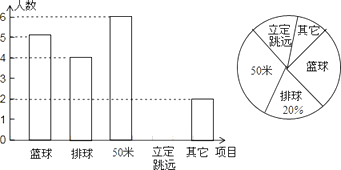
(1)本次调查共抽取了名学生;
(2)此次调查报其他项目的人数占了(填百分数),报立定跳远的人数是;
(3)扇形统计图中50米部分所对应的圆心角的度数是;
(4)我市共有初三学生3000名,估计我市有多少名学生选报篮球项目? -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校开展课外体育活动,决定开设
 :篮球、
:篮球、 :乒乓球、
:乒乓球、 :踢毽子、
:踢毽子、 :跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.(1)求出“最喜欢篮球”部分的扇形的圆心角度数;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?

相关试题

