【题目】如图,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的Bˊ点,AE是折痕. 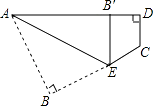
(1)试判断BˊE与DC的位置关系.
(2)如果∠C=140°,求∠AEB的度数.
参考答案:
【答案】
(1)解:由折叠的性质,得
∠B=∠AB′E=90°,
∴∠AB′E=∠C=90°,
∴B′E∥DC
(2)解:由四边形的一组对角互补,得
∠DAB+∠C=180°.
由∠C=140°得
∠DAB=180°﹣∠C=40°.
由翻折的性质,得
∠BAE= ![]() ∠DAB=
∠DAB= ![]() ×40°=20°
×40°=20°
【解析】(1)根据翻折的性质,可得∠AB′E,根据平行线的判定;(2)根据四边形的性质,可得∠DAB的度数,根据翻折的性质,可得答案.
【考点精析】利用翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市参加中考的15 000名学生的视力情况,抽取1 000名学生的视力进行统计分析,下列判断错误的是( )
A. 15 000名学生的视力是总体B. 1 000名学生是总体的一个样本
C. 每名学生的视力是总体的一个个体D. 样本容量为1 000
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:
(1)(3a5b3﹣a4b2)÷(﹣a2b)2
(2)a(3﹣a)﹣(1+a)(1﹣a) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=
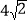 ,则△EFC的周长为( )
,则△EFC的周长为( )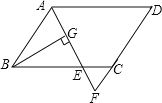
A. 11 B. 10 C. 9 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,AE平分∠BAD交BC与点E,且将BC分成4cm和6cm两部分,则平行四边形ABCD的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
(1)求证:
 ;
;(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求其最大值;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动(当点Q与点C重合时停止运动),设运动时间为t秒,矩形EFFQ与△ABC重叠部分的面积为S,求S与t的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,则a的最大值是( )
A. 480 B. 479 C. 448 D. 447
相关试题

