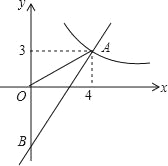
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
参考答案:
【答案】(1)y=![]() , y=2x﹣5;(2)点M的坐标为(2.5,0).
, y=2x﹣5;(2)点M的坐标为(2.5,0).
【解析】(1)利用待定系数法即可解答;
(2)设点M的坐标为(x,2x﹣5),根据MB=MC,得到![]() ,即可解答.
,即可解答.
(1)把点A(4,3)代入函数y=![]() 得:a=3×4=12,∴y=
得:a=3×4=12,∴y=![]() .OA=
.OA=![]() =5,
=5,
∵OA=OB,∴OB=5,∴点B的坐标为(0,﹣5),
把B(0,﹣5),A(4,3)代入y=kx+b得:![]() 解得:
解得:![]() ∴y=2x﹣5.
∴y=2x﹣5.
(2)∵点M在一次函数y=2x﹣5上,∴设点M的坐标为(x,2x﹣5),
∵MB=MC,∴![]()
解得:x=2.5,∴点M的坐标为(2.5,0).
“点睛”本题考查了一次函数与反比例函数的交点,解决本题的关键是利用待定系数法求解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线l:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…,则S8等于( )

A.28B.213C.216D.218
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣4x+4沿y轴向下平移9个单位,所得新抛物线与x轴正半轴交于点B,与y轴交于点C,顶点为D.求:(1)点B、C、D坐标;(2)△BCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆GF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.
(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上,
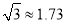 ,
, 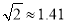 ,结果精确到0.1)
,结果精确到0.1)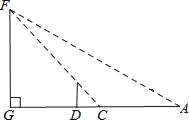
-
科目: 来源: 题型:
查看答案和解析>>【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
-
科目: 来源: 题型:
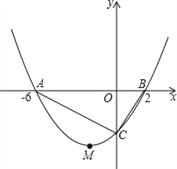
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”期间,某商场购进A、B两种品牌的粽子共320袋,其中A品牌比B品牌多80袋.此两种粽子每袋的进价和售价如下表所示,已知销售八袋A品牌的粽子获利136元.(注;利润=售价-进价)
品牌
A
B
进价(元/袋)
m
38
售价(元/袋)
66
50
(1)试求出m的值.
(2)该商场购进A、B两种品牌的粽子各多少袋?
(3)该商场调整销售策略,A品牌的粽子每袋按原售价销售,B品牌的粽子每袋打折出售.如果购进的A、B两种品牌的粽子全部售出的利润不少于4360元,问B种品牌的粽子每袋最低打几折出售?
相关试题

