【题目】某校九年级两个班,各选派10名学生参加学校举行的“诗词大赛”预赛.参赛选手的成绩如下(单位:分)
九(1)班:88,91,92,93,93,93,94,98,99,100
九(2)班:89,93,93,93,95,96,96,96,98,99.
(1)九(2)班的平均分是 分;九(1)班的众数是 分;
(2)若从两个班成绩最高的5位同学中选2人参加市级比赛,则这两个人来自不同班级的概率是多少?
参考答案:
【答案】(1)94.8、93;(2)![]() .
.
【解析】分析:(1)根据平均数的定义计算(2)班的平均数,根据众数的定义确定(1)班的众数;
(2)设九(1)学生为B1,B2,B3,九(2)学生为A1,A2,画树状图展示所有20种等可能的结果数,找出另外两个决赛名额落在不同班级的结果数,然后根据概率公式求解.
详解:(1)九(2)班的平均分为![]() 分,九(1)班的众数是93分,
分,九(1)班的众数是93分,
故答案为:94.8、93;
(2)设九(1)班学生为![]() 九(2)班学生为
九(2)班学生为![]()
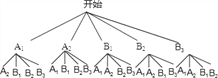
一共有20种等可能结果,其中2人来自不同班级共有12种,
所以这两个人来自不同班级的概率是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 .现点
.现点 绕着点
绕着点 以每秒
以每秒 的速度顺时针旋转一周后停止.则(1)点
的速度顺时针旋转一周后停止.则(1)点 旋转一周所用的时间是______秒;(2)同时点
旋转一周所用的时间是______秒;(2)同时点 沿线段
沿线段 自点
自点 向点
向点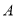 运动,假若点
运动,假若点 、
、 也能相遇,则点
也能相遇,则点 的速度是______
的速度是______ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC,BD相交于点O,∠ADB=30°,E为BC边上一点,∠AEB=45°,CF⊥BD于F.下列结论:①BE=CD,②BF=3DF,③AE=
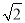 AO,④CE=CF.正确的结论有( )
AO,④CE=CF.正确的结论有( )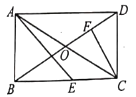
A. ①②B. ②③C. ①②④D. ①②③
-
科目: 来源: 题型:
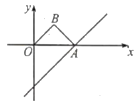
查看答案和解析>>【题目】如图,直线y=x﹣4与x轴交于点A,以OA为斜边在x轴上方作等腰Rt△OAB,并将Rt△AOB沿x轴向右平移,当点B落在直线y=x﹣4上时,Rt△OAB扫过的面积是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y =(2m+1) x+ m-3
(1) 若函数图象经过原点,求m的值.
(2) 若函数图象在y轴的交点的纵坐标为-2,求m的值.
(3)若函数的图象平行直线y=-3x–3,求m的值.
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校办公楼前有一长为
 ,宽为
,宽为 的长方形空地,在中心位置留出一个半径为
的长方形空地,在中心位置留出一个半径为 的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
(1)用含字母和
 的式子表示阴影部分的面积;
的式子表示阴影部分的面积;(2)当
 =4,
=4, =3,
=3, =1,
=1, =2时,阴影部分面积是多少?(
=2时,阴影部分面积是多少?( 取3)
取3) -
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数
54
45
30
24
21
12
人 数
1
1
2
6
3
2
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.
相关试题

