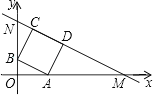
【题目】如图，已知直线y＝﹣x+b（b＞0）交x轴，y轴于点M，N，点A，B是OM，ON上的点，以AB为边作正方形ABCD，CD恰好落在MN上，已知AB＝2，则b的值为（　　）

A.1+B.C.D.2+

【答案】C

【解析】

由直线的解析式可知tan∠OMN=，根据平行线的性质和余角的性质可证∠OAB=∠OMN=∠NBC，在Rt△BCN中，求出BN=；在Rt△BOA中，求出BO=；又由b=ON即可求解．

∵直线y＝﹣x+b，

∴tan∠OMN＝，

∵正方形ABCD，

∴AB//CD，

∴∠OAB＝∠OMN，

∵∠NBC+∠ABO=90°，∠ABO+∠OAB=90°，

∴∠OAB＝∠OMN＝∠NBC，

∵AB＝2，

∴BC＝AD＝2，

在Rt△BCN中，BC＝2，tan∠NBC＝，

∴BN＝，

在Rt△BOA中，BA＝2，tan∠OAB＝，

∴BO＝，

∵b＞0，

∴b＝ON＝；

故选：C．

关闭