【题目】已知(x+3)2与|y﹣2|互为相反数,z是绝对值最小的有理数,则(x+y)y+xyz=_____.
参考答案:
【答案】1.
【解析】
根据题意z是绝对值最小的有理数可知,z=0,且互为相反数的两数和为0,注意平方和绝对值都具有非负性.
∵(x+3)2与|y2|互为相反数,
∴(x+3)2+|y2|=0,
∵(x+3)2≥0,|y2|≥0,
∴(x+3)2=0,|y2|=0,即x+3=0,y2=0,
∴x=3,y=2,
∵z是绝对值最小的有理数,∴z=0.
(x+y)y+xyz=(3+2)2+(3)×2×0=1.
故答案为:1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:
 与直线x=-2交于点P.
与直线x=-2交于点P.(1)当抛物线F经过点C时,求它的表达式;
(2)设点P的纵坐标为
 ,求
,求 的最小值,此时抛物线F上有两点
的最小值,此时抛物线F上有两点 ,
, ,且
,且 ≤-2,比较
≤-2,比较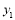 与
与 的大小;
的大小; (3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】移动互联网已经全面进入人们的日常生活,截至2016年4月,全国4G用户总数达到1.62亿,其中1.62亿用科学记数法表示为( )
A.1.62×104
B.162×106
C.1.62×108
D.0.162×109 -
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2﹣4x﹣6=0,变形正确的是( )
A. (x﹣2)2=2 B. (x﹣2)2=10 C. (x﹣4)2=22 D. (x+2)2=10
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽购买学习用品的数据如下表,因污损导致部分数据无法识别.根据下表,解决下列问题:
(1)小丽购买了自动铅笔、记号笔各几个?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?

-
科目: 来源: 题型:
查看答案和解析>>【题目】a11÷(﹣a2)3a5的值为( )
A.1B.﹣1C.﹣a10D.a9
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数,例如:[1.5]=1,[﹣2.3]=﹣3,则[﹣5.2]+[﹣0.3]+[2.2]=_____
相关试题

