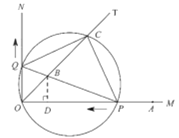
【题目】如图，已知，是的平分线，是射线上一点，．动点从点出发，以的速度沿水平向左作匀速运动，与此同时，动点从点出发，也以的速度沿竖直向上作匀速运动．连接，交于点．经过、、三点作圆，交于点，连接、．设运动时间为，其中．

（1）求的值；

（2）是否存在实数，使得线段的长度最大？若存在，求出的值；若不存在，说明理由．

（3）求四边形的面积．

【答案】（1）8cm；（2）存在，当t=4时，线段OB的长度最大，最大为；（3）

【解析】

（1）根据题意可得，，由此可求得的值；

（2）过作，垂足为，则，设线段的长为，可得，，，根据可得，进而可得，由此可得，由此可得，则可得到答案；

（3）先证明是等腰直角三角形，由此可得，再利用勾股定理可得，最后根据四边形的面积即可求得答案．

解：（1）由题可得：，．

∴．

（2）当时，线段的长度最大．

如图，过作，垂足为，则．

∵平分，

∴，

∴，．

设线段的长为，

则，，．

∵，

∴，

∴，

∴，

解得：．

∴．

∴当时，线段的长度最大，最大为．

（3）∵，

∴是圆的直径．

∴．

∵，

∴是等腰直角三角形．

∴

．

在中，．

∴四边形的面积

．

∴四边形的面积为．

关闭