【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,AB=25,顶点C在y轴的负半轴上,AO:OC=3:4,点P在线段OC上,且PO、PC的长(PO<PC)是关于x的方程x2-12x+32=O的两根.
(1) 求P点坐标求
(2) 求AC、BC的长;
(3)在x轴上是否存在点Q,使以点A、C、P、Q为顶点的四边形是梯形?若存在,请直接写出直线PQ的解析式;若不存在,请说明理由.

参考答案:
【答案】(1)P(0,-4) (2)AC=15 BC=20 (3)y=-![]() -4或y=-
-4或y=-![]() -4
-4
【解析】试题分析:(1)根据方程的解求出两根,然后跟PO<PC求出点P的坐标;(2)根据双垂直得出∠ACO=∠ABC,然后根据∠ABC的正切值求出AC和BC的长度;(3)根据等腰梯形的性质求出点Q的坐标,然后计算PQ的函数解析式.
试题解析:(1)![]() -12x+32=O.解得
-12x+32=O.解得![]() =4,
=4,![]() =8 ∵ PO<PC.
=8 ∵ PO<PC.
∴ PO=4. ∴ P(O,-4)
(2)∵ ∠ACB=90°,CO⊥AB, ∴ ∠ACO=∠ABC. ∴ tan∠ABC=![]() ,
,
Rt△ABC中,设AC=3a,BC=4a 则AB=5a,
∵AB=5a=25 ∴ a=5 ∴ AC="15" BC=20
(3)存在,直线PQ解析式为:y=-![]() -4或y=-
-4或y=-![]() -4.
-4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正六边形外接圆的半径是3,则这个正六边形的周长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,梯形的上底长是
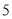 厘米,下底长是
厘米,下底长是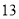 厘米,当梯形的高由大变小时,梯形的面积也随之发生变化.
厘米,当梯形的高由大变小时,梯形的面积也随之发生变化.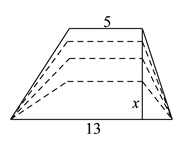
(
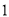 )在这个变化过程中,自变量是__________,因变量是__________.
)在这个变化过程中,自变量是__________,因变量是__________.(
 )梯形的面积
)梯形的面积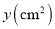 与高
与高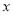 (厘米)之间的关系式为__________.
(厘米)之间的关系式为__________.(
 )当梯形的高由
)当梯形的高由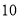 厘米变化到
厘米变化到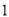 厘米时,梯形的面积由__________
厘米时,梯形的面积由__________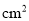 变化到__________
变化到__________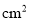 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某组7名同学在一学期里阅读课外书籍的册数分别是:14,12,13,12,17,18,16.则这组数据的众数和中位数分别是( )
A. 12,13 B. 12,14 C. 13,14 D. 13,16
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3a﹣2)﹣3(a﹣5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x1,x2,x3的平均数为3,则5x1+1,5x2+2,5x3+3的平均数为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB经过圆心O,交⊙O于点A,C,点D在⊙O上,连接AD,BD,∠A=∠B=30°.

(1)求证:BD是⊙O的切线
(2)如果BD=2求OC的长
相关试题

