搜索
【题目】如图，已知：∠BCF=∠B+∠F.求证：AB//EF .
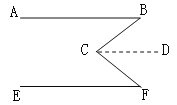
证明：经过点C作CD//AB
∴∠BCD=∠B.（ ）
∵∠BCF=∠B+∠F，（已知）
∴∠ （ ）=∠F.（ ）
∴CD//EF.（ ）
∴AB//EF（ ）
参考答案：
【答案】证明见解析.
【解析】试题分析：根据平行线的性质填第一个空；根据等式的性质填第二个空；根据平行线的判定填第三个空；根据平行公理的推论填第三个空即可．
试题解析：证明：经过点C作CD∥AB，
∴∠BCD=∠B(两直线平行,内错角相等)；
∵∠BCF=∠B+∠F,(已知)，∠BCF=∠BCD+∠DCF，
∴∠DCF=∠F(等式的性质)，
∴CD∥EF(内错角相等，两直线平行，
∴AB∥EF(平行于同一直线的两直线平行).
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边AB在数轴上，数轴上点A表示的数为﹣1，正方形ABCD的面积为16．
（1）数轴上点B表示的数为 ；
（2）将正方形ABCD沿数轴水平移动，移动后的正方形记为A′B′C′D′，移动后的正方形A′B′C′D′与原正方形ABCD重叠部分的面积为S．
①当S=4时，画出图形，并求出数轴上点A′表示的数；
②设正方形ABCD的移动速度为每秒2个单位长度，点E为线段AA′的中点，点F在线段BB′上，且BF=
BB′．经过t秒后，点E，F所表示的数互为相反数，直接写出t的值． -
科目： 来源： 题型：
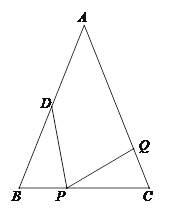
查看答案和解析>>【题目】如图，已知△ABC中，AB=AC=6cm，BC=4cm，点D为AB的中点．
⑴如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．
①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CPQ是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为______cm/s时，在某一时刻也能够使△BPD与△CPQ全等．
⑵若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都按逆时针方向沿△ABC的三边运动．求经过多少秒后，点P与点Q第一次相遇，并写出第一次相遇点在△ABC的哪条边上？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示， AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一拱形公路桥，圆弧形桥拱的水面跨度AB＝80 m，桥拱到水面的最大高度为20 m.(1)求桥拱的半径．
(2)现有一艘宽60 m，顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥，这艘轮船能顺利通过吗？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列7个事件中：（1）掷一枚硬币，正面朝上．（2）从一副没有大小王的扑克牌中抽出一张恰为黑桃．（3）随意翻开一本有400页的书，正好翻到第100页．（4）天上下雨，马路潮湿．（5）你能长到身高4米．（6）买奖券中特等大奖．（7）掷一枚正方体骰子，得到的点数＜7．其中（将序号填入题中的横线上即可）确定事件为________；不确定事件为________；不可能事件为________；必然事件为________；不确定事件中，发生可能性最大的是________，发生可能性最小的是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为弘扬中华传统文化，黔南州近期举办了中小学生“国学经典大赛”．比赛项目为：A．唐诗；B．宋词；C．论语；D．三字经．比赛形式分“单人组”和“双人组”．
（1）小丽参加“单人组”，她从中随机抽取一个比赛项目，恰好抽中“三字经”的概率是多少？
（2）小红和小明组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次，则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少？请用画树状图或列表的方法进行说明．
相关试题
