【题目】如图,在热气球上A处测得塔顶B的仰角为52°,测得塔底C的俯角为45°,已知A处距地面98米,求塔高BC.(结果精确到0.1米)
【参考数据:sin52°=0.79,cos52°=0.62,tan52°=1.28】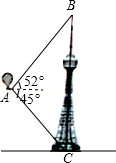
参考答案:
【答案】解:如图,过点A作AD⊥BC于点D.
由题意可知,在Rt△ADC中,
∠ADC=90°,∠CAD=45°,CD=98,
∴∠ACD=∠CAD=45°.
∴AD=CD=98.
在Rt△ABD中,
BD=AD×tan∠BAD=98×1.28=125.44.
∴BC=BD+CD=125.44+98=223.44≈223.4(米).
答:塔高BC约为223.4米.
【解析】过点A作AD⊥BC于点D,根据∠ACD=∠CAD=45°求出∠ACD=∠CAD=45°,从而得到AD=CD=98,再在Rt△ABD中,求出BC的长.
【考点精析】通过灵活运用关于仰角俯角问题,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了减少雾霾,美化环境,小王上班的交通方式由驾车改为骑自行车,小王家距单位的路程是15千米,在相同的路线上,小王驾车的速度是骑自行车速度的4倍,小王每天骑自行车上班比驾车上班要早出发45分钟,才能按原时间到达单位,求小王骑自行车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、O、B在同一条直线上.

(1)∠AOC比∠BOC大100°,求∠AOC与∠BOC的度数;
(2)在(1)的条件下,若∠BOC与∠BOD互余,求∠BOD的度数;
(3)在(1)(2)的条件下,若OE平分∠AOC,求∠DOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上A、B两点所表示的数分别为-2和8.
(1)求线段AB的长;
(2)若P为射线BA上的一点(点P不与A、B两点重合,M为PA的中点,N为PB的中点,当点P在射线BA上运动时;MN的长度是否发生改变?若不变,请你画出图形,并求出线段MN的长;若改变,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某超市举行店庆活动,对甲、乙两种商品实行打折销售。打折前,购买3件甲商品和1件乙商品需用190元;购买2件甲商品和3件乙商品需用220元。而店庆期间,购买10件甲商品和10件乙商品仅需735元,这比不打折少花多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,D是AB边上的一点,过点D作DE∥BC,∠ABC的角平分线于点E.
(1)如图1,当点E恰好在AC边上时,求证:∠ADE=2∠DEB;
(2)如图2,当点D在BA的延长线上时,其余条件不变,请直接写出∠ADE与∠DEB之间的数量关系,并说明理由。
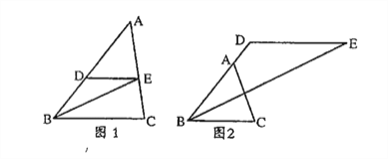
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某小区家庭用水情况,小丽随机调查了该小区部分家庭4月份的用水量,并将收集的数据整理并绘制成如下条形统计图.

(1)求小丽调查的家庭总数?
(2)所调查家庭4月份用水量的众数为吨,中位数为吨.
(3)该小区共有200户家庭,请估计这个小区4月份的用水总量.
相关试题

