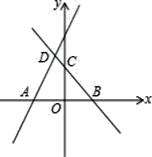
【题目】直线y=2x+m（m＞0）与x轴交于点A（﹣2，0），直线y=﹣x+n（n＞0）与x轴、y轴分别交于B、C两点，并与直线y=2x+m（m＞0）相交于点D，若AB=4．

（1）求点D的坐标；

（2）求出四边形AOCD的面积；

（3）若点P为x轴上一动点，且使PD+PC的值最小，不写过程，直接写出点P的坐标。

参考答案：

【答案】（1）D点坐标为（﹣， ）；

（2）四边形AOCD的面积=；

（3）点E的坐标为（2﹣2，0）、（﹣2﹣2，0）、（2，0）、（0，0）．

【解析】试题分析：（1）先把A点坐标代入y=2x+m得到m=4，则y=-2x+4，再利用AB=4可得到B点坐标为（2，0），则把B点坐标代入y=-x+n可得到n=2，则y=-x+2，然后根据两直线相交的问题，通过解方程组得到D点坐标；

（2）先确定C点坐标为（0，2），然后利用四边形AOCD的面积=S△DAB-S△COB进行计算即可；（3）先利用A、C两点的坐标特征得到△ACO为等腰直角三角形，AC=，然后分类讨论：当AE=AC=时，以A点为圆心，2画弧交x轴于E1点和E2点，再写出它们的坐标；当CE=CA时，E3点与点A关于y轴对称，即可得到它的坐标；当EA=EC时，E4点为坐标原点．

试题解析：（1）把A（﹣2，0）代入y=2x+m得﹣4+m=0，

解得m=4，

∴y=﹣2x+4，

∵AB=4，A（﹣2，0），

∴B点坐标为（2，0），

把B（2，0）代入y=﹣x+n得﹣2+n=0，

解得n=2，

∴y=﹣x+2，

解方程组得，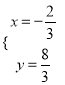

∴D点坐标为（﹣， ）；

（2）当x=0时，y=﹣x+2=2，

∴C点坐标为（0，2），

∴四边形AOCD的面积=S△DAB﹣S△COB=×4×﹣×2×2=；

（3）∵A（﹣2，0），C（0，2），

∴AC=，

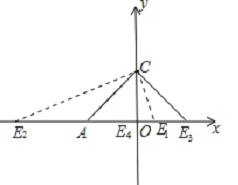
当AE=AC=时，E1点的坐标为（﹣2，0），E2点的坐标为（﹣﹣2，0）；

当CE=CA时，E3点的坐标为（2，0），

当EA=EC时，E4点的坐标为（0，0），

综上所述，点E的坐标为（﹣2，0）、（﹣﹣2，0）、（2，0）、（0，0）．

关闭