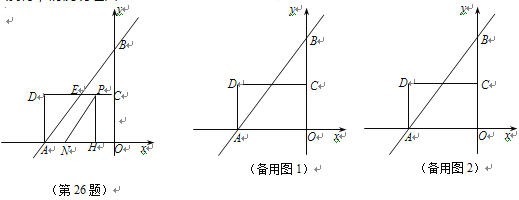
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于A,B两点,点C[]为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C[]为OB的中点,点D在第二象限,且四边形AOCD为矩形.
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作![]() ,垂足为H,连接NP.设点P的运动时间为
,垂足为H,连接NP.设点P的运动时间为![]() 秒.
秒.
①若△NPH的面积为1,求![]() 的值;
的值;
②点Q是点B关于点A的对称点,问![]() 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
参考答案:
【答案】(1) A(-3,0),B(0,4).![]() (2)①1,2②BP+PH+HQ有最小值,(-2,2)
(2)①1,2②BP+PH+HQ有最小值,(-2,2)
【解析】
试题分析:(1)让y=0求得x的值可得A的坐标,(0,b)为B的坐标,让y=![]() 可得交点的纵坐标,代入直线解析式可得交点的横坐标;
可得交点的纵坐标,代入直线解析式可得交点的横坐标;
(2)由△AMN∽△ABO,得出△MPH的面积,再利用由△HPE∽△HFM,表示出△PEH的面积,即可得出答案.
(3)当点C,H,Q在同一直线上时,CH+HQ的值最小,利用平行四边形的性质得出即可.
试题解析:(1) A(-3,0),B(0,4).
当y=2时,![]()
所以直线AB与CD交点的坐标为![]()
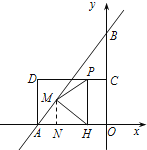
(2)①当0<t<![]() 时,
时,![]()
解得![]()
②当![]() 时,
时,![]()
解得![]()
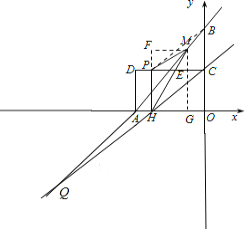
②BP+PH+HQ有最小值.
连接PB,CH,则四边形PHCB是平行四边形.
∴BP=CH.
∴BP+PH+HQ=CH+HQ+2.
当点C,H,Q在同一直线上时,CH+HQ的值最小
∵点C,Q的坐标分别为(0,2),(-6,-4),
∴直线CQ的解析式为y=x+2,
∴点H的坐标为(-2,0).因此点P的坐标为(-2,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把直线y=2x-1向左平移5个单位得到直线l,则直线l的解析式为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x2+ax可以分解因式,则常数a不可以取( )
A. ﹣1B. 0C. 1D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个棱柱有18条棱,则它有__ 个面.
-
科目: 来源: 题型:
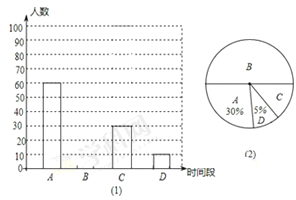
查看答案和解析>>【题目】为了了解中学生参加体育活动情况,某校对部分学生进行了调查,其中一个问题是:“你平均每天参加体育活动的时间是多少?”共有4个选项(每个时间段含最小值不含最大值):
A.1.5小时以上 B.1—1.5小时 C.0.5 —1小时 D.0.5小时以下
根据调查结果绘制了两幅不完整的统计图.请你根据以上信息解答下列问题:
(1)本次调查活动采取了 的调查方式.(填“普查”或“抽样调查”)
(2)本次调查共调查了________人,图(2)中选项C的圆心角为 ______度.
(3)请将图(1)中选项B的部分补充完整.
(4)若该校有2000名学生,你估计该校可能有_______名学生平均每天参加体育活动的时间在1小时以下.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适合采用普查方式的是( )
A. 调查一批汽车的使用寿命
B. 调查重庆市市民“五.一”期间计划外出旅游情况
C. 调查某航班的旅客是否携带了违禁物品
D. 调查全国初三学生的视力情况
-
科目: 来源: 题型:
查看答案和解析>>【题目】转基因作物是利用基因工程将原有作物基因加入其它生物的遗传物质,并将不良基因移除,从而造成品质更好的作物.我国现有转基因作物种植面积约为4 200 000公顷,将4 200 000用科学记数法表示为( )
A. 4.2×106 B. 4.2×105 C. 42×105 D. 0.42×107
相关试题

