【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.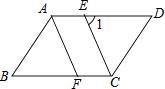
参考答案:
【答案】
(1)证明:
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,∠B=∠D,
∵AF∥CE,
∴四边形AECF为平行四边形,
∴AE=CF,
∴DE=BF,
在△ABF和△CDE中
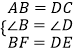
∴△ABF≌△CDE(SAS);
(2)解:
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∵AD∥BC,
∴∠BCE=∠1,
∴∠DCE=∠1=65°,
∴∠D=180°﹣65°﹣65°=50°,
∴∠B=50°.
【解析】(1)首先依据平行四边形的性质可证明AD∥BC,AD=BC,∠B=∠D,然后平行四边形的判定定理可得到四边形AECF为平行四边形,从而可证明DE=BF,最后依据SAS进行证明即可;
(2)由角平分线的定义和平行线的性质可证得∠1=∠DCE,则可求得∠D,最后,依据平行四边形对角相等可求得∠B的度数.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:长方形ABCD在坐标平面内的位置如图所示, A(1,1) C(-3,-4),点P从点A出发,沿着A→B→C→D→A的路径,以每秒
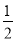 个单位的速度运动.运动一周回到A点时停止运动.设运动时间为t秒.
个单位的速度运动.运动一周回到A点时停止运动.设运动时间为t秒.
(1)直接写出点B、点D的坐标.
(2)当t=6秒时,写出P点的坐标.
(3)当点P运动到与x轴的距离为
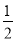 个单位时直接写出t的值.
个单位时直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
(1)自己画出图形并解答:A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(2)求证:无论m取何值,函数y=mx﹣2(m﹣1)的图象经过的一个确定的点;
(3)若(1),(2)中两图象围成图形的面积刚好为2,求m值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某开发区有一块四边形的空地
 ,如图所示,现计划在空地上种植草皮,经测量
,如图所示,现计划在空地上种植草皮,经测量 ,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
-
科目: 来源: 题型:
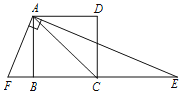
查看答案和解析>>【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于
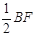 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.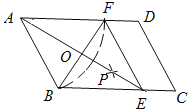
(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
相关试题

