【题目】某商场在一楼与二楼之间装有一部自动扶梯,以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯上走到二楼(扶梯本身也在行驶).如果二人都做匀速运动,且男孩每分钟走动的级数是女孩的两倍.又已知男孩走了27级到达顶部,女孩走了18级到达顶部(二人每步都只跨1级).
(1)扶梯在外面的部分有多少级.
(2)如果扶梯附近有一从二楼下到一楼的楼梯,台阶级数与扶梯级数相等,这两人各自到扶梯顶部后按原速度走下楼梯,到一楼后再乘坐扶梯(不考虑扶梯与楼梯间的距离).则男孩第一次追上女孩时,他走了多少台阶?
参考答案:
【答案】(1)楼梯有54级(2) 198级
【解析】【试题分析】
(1)设女孩速度为![]() 级/分,电梯速度为
级/分,电梯速度为![]() 级/分,楼梯(扶梯)为
级/分,楼梯(扶梯)为![]() 级,则男孩速度为
级,则男孩速度为![]() 级/分, 根据时间相等列方程,有:
级/分, 根据时间相等列方程,有:
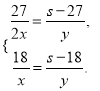 ①两式相除,得
①两式相除,得![]() ,解方程得
,解方程得![]() 即可.
即可.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯![]() 次,走过楼梯
次,走过楼梯![]() 次,则这时女孩走过扶梯
次,则这时女孩走过扶梯![]() 次,走过楼梯
次,走过楼梯![]() 次.
次.
将![]() 代入方程组①,得
代入方程组①,得![]() ,即男孩乘扶梯上楼的速度为
,即男孩乘扶梯上楼的速度为![]() 级/分,女孩乘扶梯上楼的速度为
级/分,女孩乘扶梯上楼的速度为![]() 级/分.于是有
级/分.于是有
![]() 从而
从而![]() ,即
,即![]() .
.
无论男孩第一次追上女孩是在扶梯上还是在下楼时, ![]() 中必有一个为正整数,且
中必有一个为正整数,且![]() ,经试验知只有
,经试验知只有![]() 符合要求.
符合要求.
这时,男孩第一次追上女孩所走过的级数是: ![]() (级).
(级).
【试题解析】
(1)设女孩速度为![]() 级/分,电梯速度为
级/分,电梯速度为![]() 级/分,楼梯(扶梯)为
级/分,楼梯(扶梯)为![]() 级,则男孩速度为
级,则男孩速度为![]() 级/分,依题意有
级/分,依题意有
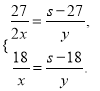 ①
①
把方程组①中的两式相除,得![]() ,解得
,解得![]() .
.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯![]() 次,走过楼梯
次,走过楼梯![]() 次,则这时女孩走过扶梯
次,则这时女孩走过扶梯![]() 次,走过楼梯
次,走过楼梯![]() 次.
次.
将![]() 代入方程组①,得
代入方程组①,得![]() ,即男孩乘扶梯上楼的速度为
,即男孩乘扶梯上楼的速度为![]() 级/分,女孩乘扶梯上楼的速度为
级/分,女孩乘扶梯上楼的速度为![]() 级/分.于是有
级/分.于是有
![]()
从而![]() ,即
,即![]() .
.
无论男孩第一次追上女孩是在扶梯上还是在下楼时, ![]() 中必有一个为正整数,且
中必有一个为正整数,且![]() ,经试验知只有
,经试验知只有![]() 符合要求.
符合要求.
这时,男孩第一次追上女孩所走过的级数是: ![]() (级).
(级).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(a,a+5)在x轴上,则点A到原点的距离为( )
A.﹣5B.0C.5D.不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(﹣3,﹣5)所在的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少?
(2)谁的购货方式更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为<x>,即当n为非负整数时,若
 ,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:①<1.493>=1;
②<2x>=2<x>;
③若
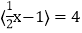 ,则实数x的取值范围是
,则实数x的取值范围是 ;
;④当x≥0,m为非负整数时,有
 ;
;⑤
 。
。其中,正确的结论有 (填写所有正确的序号)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(2k+3)x+k2=0有两个不相等的实数根x1 , x2 .
(1)求k的取值范围;
(2)若两不相等的实数根满足x1x2﹣x12﹣x22=﹣9,求实数k的值.
相关试题

