搜索
【题目】如图，已知双曲线 
， 
，点P为双曲线 
上的一点，且PA⊥x轴于点A，PB⊥y轴于点B，PA、PB分别依次交双曲线 
于D、C两点，则△PCD的面积为 ． 
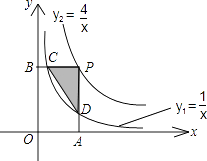
参考答案：
【答案】
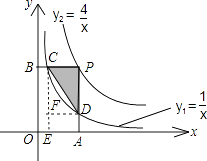
【解析】解：作CE⊥AO于E，DF⊥CE于F， ∵双曲线 
， 
，且PA⊥x轴于点A，PB⊥y轴于点B，PA、PB分别依次交双曲线 
于D、C两点，
∴矩形BCEO的面积为：xy=1，
∵BC×BO=1，BP×BO=4，
∴BC= 
BP，
∵AO×AD=1，AO×AP=4，
∴AD= AP，
∵PAPB=4，
∴ 
PB× PA= 
PAPB=CP×DP= ×4= 
，
∴△PCD的面积为： ．
所以答案是： ．
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识，掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】端午节期间，某食品店平均每天可卖出300只粽子，卖出1只粽子的利润是1元．经调查发现，零售单价每降0.1元，每天可多卖出100只粽子．为了使每天获取的利润更多，该店决定把零售单价下降m(0<m<1)元．
(1)零售单价下降m元后，该店平均每天可卖出___只粽子，利润为___元；
(2)在不考虑其他因素的条件下，当m定为多少时，才能使该店每天获取的利润是420元，并且卖出的粽子更多？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，BC交⊙O于点D，DE⊥AC于点E，要使DE是⊙O的切线，还需补充一个条件，则补充的条件不正确的是（ ）
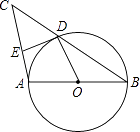
A.DE=DO
B.AB=AC
C.CD=DB
D.AC∥OD -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把一张长是a，宽是b的长方形硬纸板的四周各剪去一个边长为c的正方形（a＞b＞2c）．再折合成一个无盖的长方体盒子（纸板的厚度忽略不计）．
（1）若a=12，b=7，c=2，求折合成的长方体盒子的侧面积是多少？
（2）请用含a，b，c的代数式表示折成的长方体盒子的底面周长；
（3）如果把长方体硬纸板的四周剪去2个边长为c的正方形和2个同样形状、同样大小的长方形，然后折合成一个有盖的长方体盒子，那么它的底面周长是多少？（用含a，b，c的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】小张第一次用180元购买了8套儿童服装，以一定价格出售.如果以每套儿童服装80元的价格为标准，超出的记作整数，不足的记作负数，记录如下（单位：元）：
请通过计算说明：
（1）小张卖完这8套儿童服装后是盈利还是亏损？盈利（或亏损）了多少钱？
（2）每套儿童服装的平均售价是多少元？
（3）小张第二次用第一次的进价再次购买900元的儿童服装，如果他预计第二次每套服装的平均售价75元，按他的预计第二次售价可获利多少元？
-
科目： 来源： 题型：
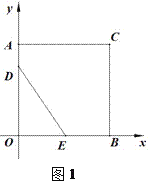
查看答案和解析>>【题目】已知，如图：在直角坐标系中，正方形AOBC的边长为4，点D、E分别是线段AO，OC上的动点，D点由A点向O点运动，速度为每秒1个单位，E点由B点向O点运动，速度为每秒2个单位，当一个点停止运动时，另一个点也随之停止.设运动时间为t（秒）
（1）如图1，当t为何值时，△DOE的面积为6；
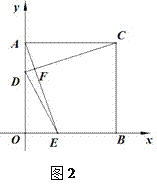
（2）如图2，连结CD,AE交于点F，当t为何值时，CD⊥AE；
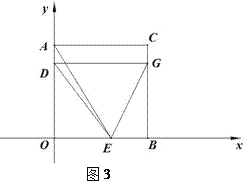
（3）如图3,过点D作DG//OB，交BC于点G，连结EG,当D，E在运动过程中，直角坐标系中是否存在点H，使得点D,E,H,G四点构成的四边形为菱形？若存在，求出t的值，并直接写出点G的坐标，若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在学习了数轴后，小亮决定对数轴进行变化应用：
（1）应用一：已知点A在数轴上表示为
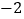，数轴上任意一点B表示的数为
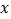，则AB两点的距离可以表示为 ；应用这个知识，请写出当
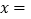时，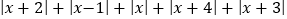
有最小值为 .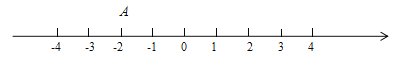
（2）应用二：从数轴上取下一个单位长度的线段，第一次剪掉原长的
，第二次剪掉剩下的，依次类推，每次都剪掉剩下的，则剪掉5次后剩下线段长度为 ；应用这个原理，请计算：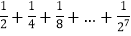
.（3）应用三：如图，将一根拉直的细线看作数轴，一个三边长分别为
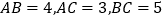的三角形
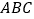的顶点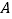
与原点重合，
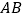边在数轴正半轴上，将数轴正半轴的线沿
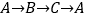的顺序依次缠绕在三角形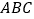的边上，负半轴的线沿
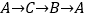的顺序依次缠绕在三角形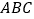的边上.①如果正半轴的线缠绕了5圈，负半轴的线缠绕了3圈，求绕在点
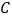上的所有数之和；②如果正半轴的线不变，将负半轴的线拉长一倍，即原线上的点
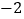的位置对应着拉长后的数
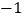，并将三角形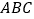向正半轴平移一个单位后再开始绕，求绕在点
且绝对值不超过100的所有数之和.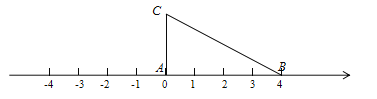
相关试题
