【题目】如图所示，已知∠ABC+∠C=180°，BD平分∠ABC，∠CBD与∠D相等吗？请说明理由．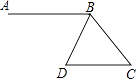

参考答案：

【答案】解：∠CBD与∠D相等； ∵∠ABC+∠C=180°，
∴AB∥DC，
∴∠D=∠ABD，
∵BD平分∠ABC，
∴∠ABD=∠DBC，
∴∠D=∠DBC．
【解析】∠CBD与∠D相等；首先根据∠ABC+∠C=180°可以根据同旁内角互补，两直线平行可得AB∥DC，再根据平行线的性质可得∠D=∠ABD，然后根据角平分线的性质可得∠CBD与∠D相等．
【考点精析】根据题目的已知条件，利用平行线的判定与性质的相关知识可以得到问题的答案，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质．

关闭