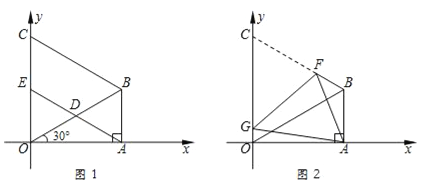
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
参考答案:
【答案】(1)B的坐标为(![]() ,4);(2)证明见解析;(3)1.
,4);(2)证明见解析;(3)1.
【解析】
试题分析:(1)由在△ABO中,∠OAB=90°,∠AOB=30°,OB=8,根据三角函数的知识,即可求得AB与OA的长,即可求得点B的坐标;
(2)首先可得CE∥AB,D是OB的中点,根据直角三角形斜边的中线等于斜边的一半,可证得BD=AD,∠ADB=60°,又由△OBC是等边三角形,可得∠ADB=∠OBC,根据内错角相等,两直线平行,可证得BC∥AE,继而可得四边形ABCD是平行四边形;
(3)首先设OG的长为x,由折叠的性质可得:AG=CG=8﹣x,然后根据勾股定理即可求得OG的长.
试题解析:(1)解:在△OAB中,∠OAB=90°,∠AOB=30°,OB=8,∴OA=OBcos30°=![]() =
=![]() ,AB=OBsin30°=8×
,AB=OBsin30°=8×![]() =4,∴点B的坐标为(
=4,∴点B的坐标为(![]() ,4);
,4);
(2)证明:∵∠OAB=90°,∴AB⊥x轴,∵y轴⊥x轴,∴AB∥y轴,即AB∥CE,∵∠AOB=30°,∴∠OBA=60°,∵DB=DO=4,∴DB=AB=4,∴∠BDA=∠BAD=120°÷2=60°,∴∠ADB=60°,∵△OBC是等边三角形,∴∠OBC=60°,∴∠ADB=∠OBC,即AD∥BC,∴四边形ABCE是平行四边形;
(3)解:设OG的长为x,∵OC=OB=8,∴CG=8﹣x,由折叠的性质可得:AG=CG=8﹣x,在Rt△AOG中,![]() ,即
,即![]() ,解得:x=1,即OG=1.
,解得:x=1,即OG=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】福建省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.
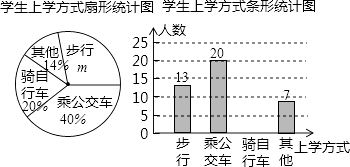
(1)m=%,这次共抽取名学生进行调查;并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
(3)如果该校共有6000名学生,请你估计该校骑自行车上学的学生有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】今年清明小长假期问,长春净月某景区接待游客约为51700人次,数字51700用科学记数法表示为( )
A.51.7×103B.5.17×104C.5.17×105D.0.517×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】36的算术平方根是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:5x2﹣20=
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解一批圆珠笔芯的使用寿命,应采用的合适的调查方式为________________.(选填“全面调查”或“抽样调查”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣b2=5,a+b=﹣2,那么代数式a﹣b的值 .
相关试题

