【题目】在△ABC中,AB=AC.
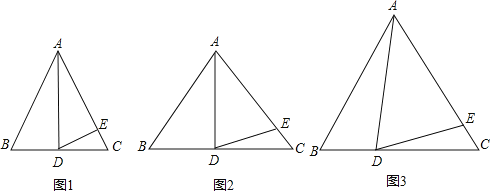
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.
参考答案:
【答案】(1)15°;(2)20°;(3)∠EDC=![]() ∠BAD;(4)仍成立,理由见解析.
∠BAD;(4)仍成立,理由见解析.
【解析】
试题分析:(1)等腰三角形三线合一,所以∠DAE=30°,又因为AD=AE,所以∠ADE=∠AED=75°,所以∠DEC=15°.
(2)同理,易证∠ADE=70°,所以∠DEC=20°.
(3)通过(1)(2)题的结论可知,∠BAD=2∠EDC(或∠EDC=![]() ∠BAD).
∠BAD).
(4)由于AD=AE,所以∠ADE=∠AED,根据已知,易证∠BAD+∠B=2∠EDC+∠C,而B=∠C,所以∠BAD=2∠EDC.
解:(1)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=30°,
∴∠BAD=∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠EDC=15°.
(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=40°,
∴∠BAD=∠CAD=40°,
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠EDC=20°.
(3)∠BAD=2∠EDC(或∠EDC=![]() ∠BAD)
∠BAD)
(4)仍成立,理由如下
∵AD=AE,∴∠ADE=∠AED,
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC
=2∠EDC+∠C
又∵AB=AC,
∴∠B=∠C
∴∠BAD=2∠EDC.
故分别填15°,20°,∠EDC=![]() ∠BAD
∠BAD
-
科目: 来源: 题型:
查看答案和解析>>【题目】服装店销售某款服装,一件服装的标价为300元,若按标价的八折销售,仍可获利50%,则这款服装每件的进价是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据为0,3,8,15,24,…则第n个数据表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划开设4门选修课:音乐、绘画、体育、舞蹈,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门),对调查结果进行统计后,绘制了如下不完整的两个统计图.
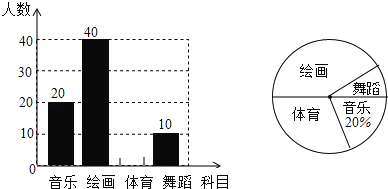
根据以上统计图提供的信息,回答下列问题:
(1)此次调查抽取的学生人数为a= 人,其中选择“绘画”的学生人数占抽样人数的百分比为b= ;
(2)补全条形统计图;
(3)若该校有2000名学生,请估计全校选择“绘画”的学生大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=x2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=x2﹣3x+5,则( )
A.b=3,c=7B.b=6,c=3C.b=﹣9,c=﹣5D.b=﹣9,c=21
-
科目: 来源: 题型:
查看答案和解析>>【题目】8.下列语句中不正确的有( )
①相等的圆心角所对的弧相等②平分弦的直径垂直于弦③圆是轴对称图形,任何一条直径都是它的对称轴④长度相等的两条弧是等弧
A.3个B.2个 C.1个 D.以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】一棵小树被风刮歪了,小明用三根木棒撑住这棵小树,他运用数学知识是三角形具有_____性.
相关试题

