【题目】已知关于x的一元二次方程(a﹣1)x2﹣2x+1=0有两个不相等的实数根,则a的取值范围是 .
参考答案:
【答案】a<2且a≠1
【解析】解:∵关于x的一元二次方程(a﹣1)x2﹣2x+l=0有两个不相等的实数根, ∴△=b2﹣4ac>0,即4﹣4×(a﹣1)×1>0,
解这个不等式得,a<2,
又∵二次项系数是(a﹣1),
∴a≠1.
故a的取值范围是a<2且a≠1.
本题是根的判别式的应用,因为关于x的一元二次方程(a﹣1)x2﹣2x+l=0有两个不相等的实数根,所以△=b2﹣4ac>0,从而可以列出关于a的不等式,求解即可,还要考虑二次项的系数不能为0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将12.348用四舍五入法取近似数,精确到0.01,其结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若amb3与﹣3a2bn是同类项,则mn= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
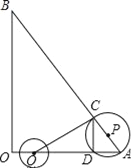
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m2﹣2m=﹣3,则8﹣2m2+4m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:

①在岸边确定一点C,使C与A,B在同一直线上;
②在AC的垂直方向画线段CD,取其中点O;
③画DF⊥CD使F、O、A在同一直线上;
④在线段DF上找一点E,使E与O、B共线.
他说测出线段EF的长就是船B与码头A的距离.他这样做有道理吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.

相关试题

