【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
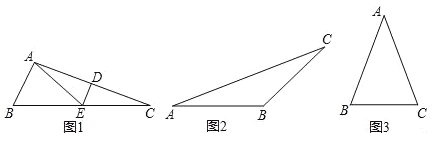
(1)如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线.
(2)如图2,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数.
(3)如图3,△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角度数为整数,请求出其特异线的长度;若它的顶角度数不是整数,请直接写出顶角度数.
参考答案:
【答案】(1)AE是△ABC是一条特异线
(2)符合条件的∠ABC的度数为135°或112.5°或140°.
(3)若它的顶角度数不是整数,则顶角度数为(![]() )°.
)°.
【解析】
试题分析:(1)只要证明△ABE,△AEC是等腰三角形即可.
(2)如图2中,当BD是特异线时,分三种情形讨论,如图3中,当AD是特异线时,AB=BD,AD=DC根据等腰三角形性质即可解决问题,当CD为特异线时,不合题意.
(3)如图3中,当BD是特异线时,分两种情形讨论即可.当AD是特异线时,不合题意.
试题解析:(1)证明:如图1中,
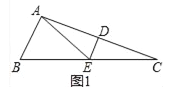
∵DE是线段AC的垂直平分线,
∴EA=EC,即△EAC是等腰三角形,
∴∠EAC=∠C,
∴∠AEB=∠EAC+∠C=2∠C,
∵∠B=2∠C,
∴∠AEB=∠B,即△EAB是等腰三角形,
∴AE是△ABC是一条特异线.
(2)如图2中,
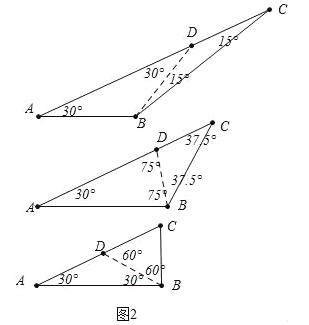
当BD是特异线时,如果AB=BD=DC,则∠ABC=∠ABD+∠DBC=120°=15°=135°,
如果AD=AC,DB=DC,则∠ABC=∠ABD+∠DBC=75°+37.5°=112.5°,
如果AD=DB,DC=DB,则ABC=∠ABD+∠DBC=30°+60°=90°(不合题意舍弃).
如图3中,当AD是特异线时,AB=BD,AD=DC,则∠ABC=180°﹣20°﹣20°=140°
当CD为特异线时,不合题意.
∴符合条件的∠ABC的度数为135°或112.5°或140°.
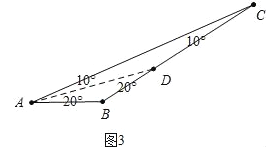
(3)如图3中,
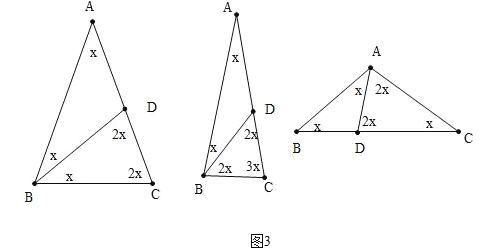
当BD是特异线时,有两种情形,如果AD=BD=BC,设∠A=x,则x+2x+2x=180°,解得x=36°,
设AD=BD=BC=a,
由△BCD∽△ABC得到![]() ,
,
∴![]() ,
,
∴a2+2a﹣4=0,
∴a=﹣1+![]() 或﹣1﹣
或﹣1﹣![]() (舍弃).
(舍弃).
如果AD=BC,BC=CD,设∠A=x,则2x+2x+3x=180°解得x=(![]() )°.
)°.
当AD是特异线时,如果DA=DB,CA=CD,设∠B=∠C=x,则x+2x+2x=180°,解得x=36°,
∴∠BAC=108°,不符合题意.
∴△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角度数为整数,其特异线的长度为﹣1+![]() ,
,
若它的顶角度数不是整数,则顶角度数为(![]() )°.
)°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,消费者在网店购买某种商品后,对其有“好评”“中评”“差评”的三种评价.小明对一家网店销售某种商品显示的评价信息进行了统计,并列出了两幅不完整的统计图.
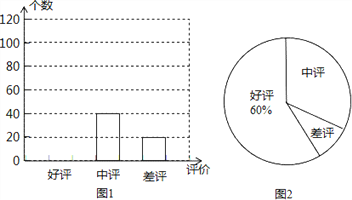
利用图中所提供的信息解决以下问题:
(1)小明一共统计了多少个评价?
(2)请将条形统计图补充完整;
(3)计算扇形统计图中“差评”所在扇形的圆心角度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,能成为一个三角形的三条边长的是( )
A. 2,3,4B. 2,2,4C. 1,2,3D. 1,2,6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,不是轴对称图形的是( )
A.一条线段
B.两条相交直线
C.有公共端点的两条相等的线段
D.有公共端点的两条不相等的线段 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在等边三角形ABC中,点D是边BC的中点,AC=8,则BD=______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A的坐标是(3,0),AB=5.
(1)当B点在x轴上时,求B点的坐标;
(2)当AB//y轴时,求B点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽与小明在讨论问题:
小丽:如果你把7498近似到4位数,你就会得到7000.
小明:不,我有另外一种解答方法,可以得到不同的答案,首先,将7498近似到百位,得到7500,接着再把7500近似到千位,就得到8000.
你怎样评价小丽和小明的说法呢?
相关试题

