【题目】如图，抛物线，直线与抛物线、轴分别相交于、．

（1）时，点的坐标为________；

（2）当、两点重合时，求的值；

（3）当点达到最高时，求抛物线解析式；

（4）在抛物线与轴所围成的封闭图形的边界上，我们把横坐标是整数的点称为“可点”，直接写出时“可点”的个数为____．

【答案】（1）（2，2）；（2）；（3）；（4）6或7或8.

【解析】

（1）当t=1时，分别求出抛物线和直线解析式，求出交点Q的坐标即可；

（2）当P，Q两点重合时，则直线l与抛物线交于x轴，交点的纵坐标为0，代入求出t的值即可；

（3）抛物线的顶点坐标是（t，t+2），当Q点达到最高时，则直线l与抛物线交于顶点，2t=t，解出t，求出解析式即可；

（4）①当t=1时，，②当t=2时，，③当时，分别求出“可点”的个数即可.

（1）当t=1时，抛物线，直线，

联立，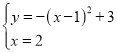

解得，

∴Q点坐标为（2，2）；

（2）当P，Q两点重合时，则直线l与抛物线交于x轴，

∴交点的纵坐标为0，

∴，

解得：；

（3）抛物线的顶点坐标是（t，t+2），

当Q点达到最高时，则直线l与抛物线交于顶点，

∴2t=t，

∴t=0，

∴抛物线解析式为：；

（4）①当t=1时，，与x轴交于A,B两点，

令y=0，得，

解得：，

∴，

∴“可点”的个数为6；

②当t=2时，，与x轴交于A,B两点，

令y=0，得，

解得：，

∴AB=4，

∴“可点”的个数为8；

③当时，

知AB＜4，

∴当抛物线不过点（3,0）时，

∴“可点”的个数为6；

∴当抛物线过点（3,0）时，

∴“可点”的个数为7；

∴时“可点”的个数为6或7或8.

关闭